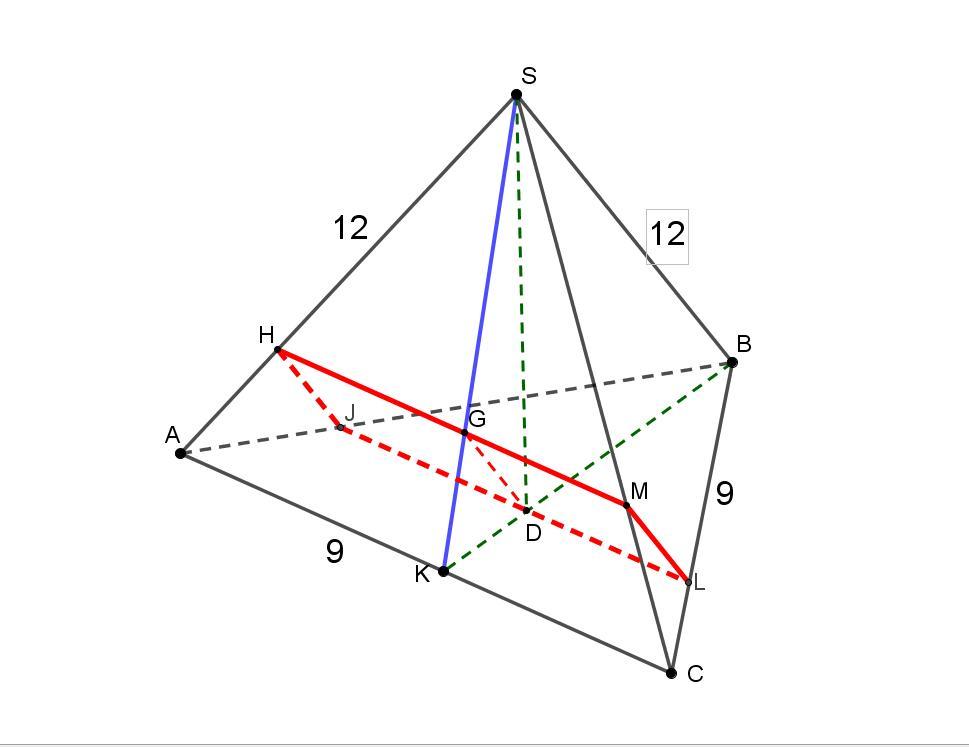
Побудуйте переріз правильної трикутної піраміди площиною, яка проходить через основу її висоти паралельно мимобіжним ребрам піраміди. Знайдіть периметр цього перерізу, якщо сторона основи піраміди дорівнює 9 см, а бічне ребро 12 см.
пожалуйста подскажите как решить , очень нужно прямо сейчас
ДАЮ 50балов
Ответы
Ответ :
30°
Объяснение:
Пусть TABC - правильная треугольная
пирамида, у которой ТО- высота, АВ+АС+ВС=6см, TB=4 см. Надйо найти угол наклона бокового ребра пирамиды к Плоскости основания.
Т.ко. ОВ- проекция ТВ на (ABC), то Искомый угол сТВО.
Его можно найти, зная ОВ, a OB=AB*√3/3=6*√3/3=2√3, как радиус описанной окружности.
COS<TBO=OB/TB=2√3/4=√3/2
значит, <ТВO=30°
Используем свойство – в правильном треугольнике
точка пересечения высот (они же и биссектрисы и медианы) делит их в отношении 1 : 2.
Эта же пропорция сохранится и для сторон треугольников, полученных при проведении прямых, параллельных скрещивающимся сторонам пирамиды.
Получаем подобные треугольники, откуда определяем длины сторон четырёхугольника в сечении.
HJ = ML = (1/3)*12 = 4 см.
HM = GL = (1/3)*9 = 3 см.
Ответ: периметр равен 2*4+2*3 = 14 см.