НА ГРАНИ ОТЧИСЛЕНИЯ, ПОМОГИТЕ ПОЖАЛУЙСТА!
Площа бічної поверхні правильної трикутної піраміди
дорівнює 90 см2
. Знайдіть апофему і висоту піраміди, якщо
сторона основи піраміди дорівнює 6 см.
Площадь боковой поверхности правильной треугольной пирамиды
равно 90 см2
. Найдите апофему и высоту пирамиды, если
сторона основания пирамиды равна 6 см.
Ответы
Ответ дал:
1
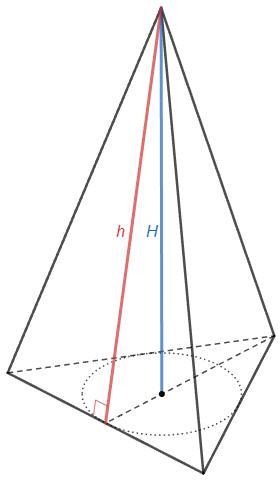
Правильная пирамида, боковые грани - равные треугольники.
Площадь боковой грани 90/3=30
30=1/2 6 h => h=10 см (h - апофема, т.е. высота боковой грани)
Высота правильной пирамиды падает в центр основания.
Радиус вписанной окружности основания r=√3/6 ·6=√3
H =√(h^2-r^2) =√(100-3) =√97 см
Приложения:
Аноним:
Я извиняюсь, а не так случайно ? https://imgur.com/a/V8H4zVn
вы нашли высоту основания, AK=3√3
дальше надо OK=AK/3=√3 и SO=√(SK^2-OK^2)=√97
Вас заинтересует
2 года назад
2 года назад
2 года назад
7 лет назад
9 лет назад