Бісектриса кута в паралелограма ABCD ділить сторону AD на два відрізки АК і KD так, що AK : KD = 4:3. Знайдіть сторони паралелограма, якщо його периметр дорівнює 66 см.
Даю 40 балов
Ответы
Ответ:
Стороны параллелограмма равны:
АВ = CD = 12 см, ВС = AD = 21 см.
Объяснение:
Биссектриса угла B параллелограмма ABCD делит сторону AD на два отрезка АК и KD так, что AK : KD = 4:3. Найдите стороны параллелограмма, если его периметр равен 66 см.
Дано: ABCD - параллелограмм;
ВК - биссектриса ∠В;
AK : KD = 4 : 3;
Р(ABCD) = 66 см.
Найти: стороны ABCD.
Решение:
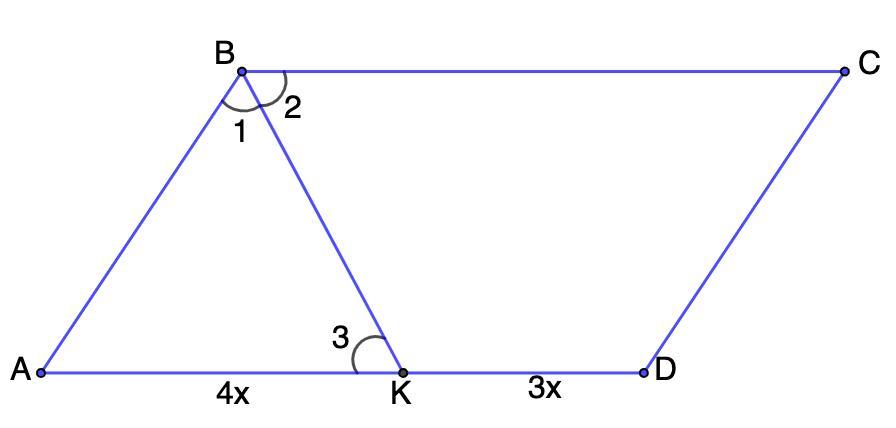
Для удобства обозначим углы цифрами (см. рис.)
∠1 = ∠2 (ВК - биссектриса)
∠3 = ∠2 (накрест лежащие при ВС || AD и секущей ВК)
⇒ ∠1 = ∠3
Рассмотрим ΔАВК.
∠1 = ∠3
- Если в треугольнике равны два угла, то этот треугольник равнобедренный.
⇒ АК = АВ.
AK : KD = 4 : 3 (условие)
Пусть АК = 4х, KD = 3х.
Тогда АК = АВ = 4х, AD = AK + KD = 4x + 3x = 7x.
- Периметр параллелограмма равен удвоенной сумме смежных сторон.
Р(ABCD) = 2(АВ + AD)
66 = 2(4x + 7x) |:2
11x = 33 |:11
x = 3
AB = 4x = 12 (см)
AD = 7x = 21 (см)
- Противоположные стороны параллелограмма равны.
⇒ АВ = CD = 12 см, ВС = AD = 21 см.
#SPJ1