Question

Решитееее пожалуйста в тетради или с об’яснением прошу вас . Знайдіть кут між меншою
стороною і діагоналлю
прямокутника, якщо він на 15°
менший від кута між
діагоналями, який лежить проти
меншої сторони.

Answer 1

Ответ:

55°

Объяснение:

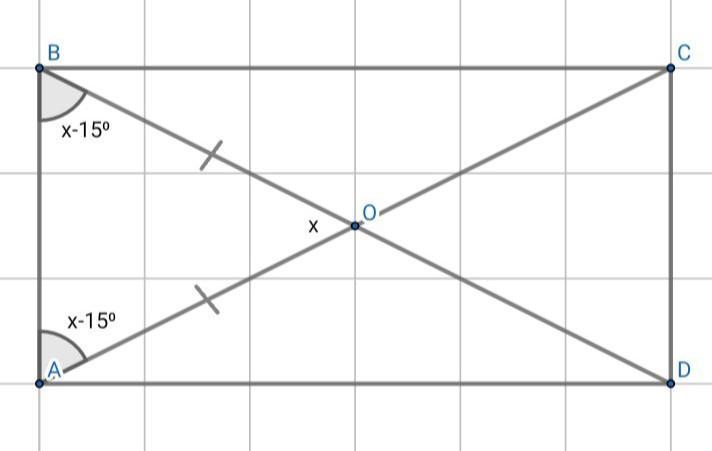
Дано: АВСD-прямоугольник , О-точка пересечения диагоналей , ∠ВАО < ∠ВОА на 15°

Найти: ∠ВОА

Решение:

Диагонали прямоугольника точкой пересечения делятся пополам ⇒ АО = ВО , значит , ∆АВО-равнобедренный , ∠ОАВ = ∠ОВА .

Возьмём ∠ОАВ и ∠ОВА за "x-15" , a ∠BOA за "x" , сумма углов треугольника должно составлять 180° .

Составим уравнение:

x + x - 15 + x - 15 = 180

3x - 30 = 180

3x = 180 + 30

3x = 210

x = 70

∠ВОА = 70° , тогда ∠OBA = x - 15° = 70° - 15° = 55°