Ответы
Ответ дал:
1
Ответ:
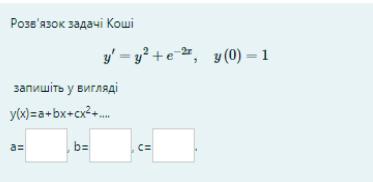
a=1; b=2; c=1.
Пошаговое объяснение:
Дано дифференциальное уравнение с начальным условием
Предполагая, что решение раскладывается в абсолютно сходящийся степенной ряд (ряд Тейлора) в окрестности нуля, нужно найти три первых члена разложения.
Имеем: причем
Первый коэффициент дает нам начальное условие: a=y(0)=1.
Второй коэффиент мы находим благодаря уравнению:
Третий коэффициент мы находим, продифференцировав уравнение:
Таким образом,
ed05080408:
Извините, не могли бы Вы мне ещё решить подубную задач?
Вас заинтересует
2 года назад
2 года назад
2 года назад
7 лет назад
7 лет назад
9 лет назад
9 лет назад