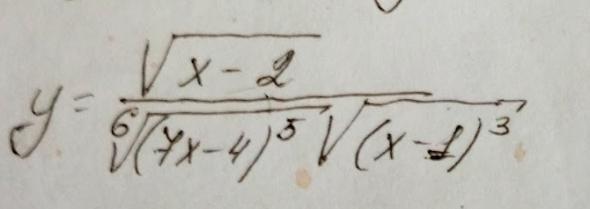Ответы
Ответ дал:
0
Решение .
Логарифмическое дифференцирование.
Прологарифмируем равенство .
Теперь найдём производные от левой и правой частей равенства ,
применив формулу .
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
7 лет назад
7 лет назад