Question

СРОЧНО

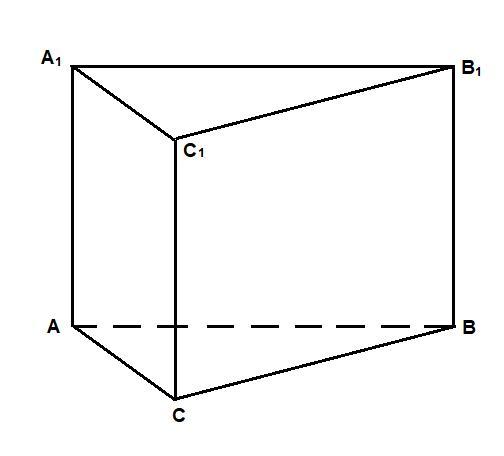
Найдите площадь боковой поверхности и площадь полной поверхности правильной треугольной призмы, сторона основы которой 8 см, а высота призмы 12 см

Answer 1

Ответ:

Площадь боковой поверхности: 288 см².

Площадь полной поверхности: 288 + 32√3 см².

Пошаговое объяснение:

Призма правильная, значит в основании лежит правильный треугольник, а боковые грани - равные прямоугольники.

• Площадь боковой поверхности правильной призмы равна произведению периметра основания на боковое ребро.

S₁ = Росн. · АА₁ = 3АВ · АА₁

S₁ = 3 · 8 · 12 = 288 см²

По формуле площади правильного треугольника найдем площадь основания:

$S_{ABC}=\dfrac{AB^2\sqrt{3}}{4}=\dfrac{8^2\sqrt{3}}{4}=\dfrac{64\sqrt{3}}{4}=16\sqrt{3}$  см²

• Площадь полной поверхности равна сумме площади боковой поверхности и двух площадей оснований:

$S=S_1+2\cdot S_{ABC}$

S = 288 + 2 · 16√3 = 288 + 32√3 см²