Question

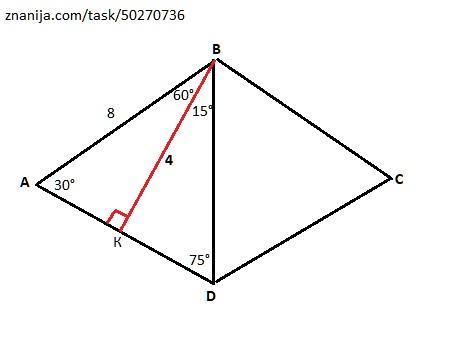
З вершини тупого кута B ромба ABCD проведено висоту BK до сторони AD. Кут KBD дорівнює 15°. Знайдіть висоту BK, якщо периметр ромба дорівнює 32 см

Answer 1

Ответ:

ВК = 4 см.

Объяснение:

В прямоугольном треугольнике ВКD ∠BDK = 75° (по сумме острых углов 90° - 15° = 75°)

В ромбе диагонали являются биссектрисами углов, а противоположные углы равны. Следовательно,

∠В = ∠D = 75·2 = 150°, а ∠АВК = (150°:2) - 15° = 75° - 15° = 60°.

В прямоугольном треугольнике АВК угол ∠А = 30° (по сумме острых углов: 90° - 60° = 30° ). Сторона АВ (гипотенуза треугольника АВК) равна 32:4 = 8 см (все стороны ромба равны, а периметр равен 32 см). Следовательно, катет ВК равен 8:2 = 4 см (как катет лежащий против угла 30°).