Ответы
Ответ дал:
2
Ответ:
Длина диагонали BD равна 14 см.
Объяснение:
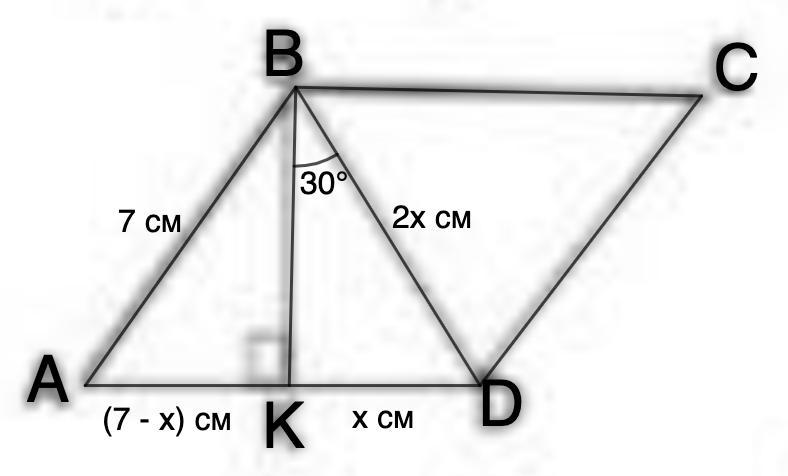
Угол между высотой и диагональю ромба, проведенных из одной вершины, равен 30°. Найти длину диагонали BD, если сторона ромба равна 7 см.
Дано: ABCD - ромб;
BD - диагональ; ВК - высота;
∠KBD = 30°; AB = 7 см.
Найти: BD.
Решение:
1. Рассмотрим ΔКВD - прямоугольный.
Пусть KD = x см, тогда АК = (7 - х) см.
∠KBD = 30°.
- Катет, лежащий против угла в 30°, равен половине гипотенузы.
⇒ BD = 2x см.
По теореме Пифагора:
BK²=BD² - KD² = 4x² - x² = 3x²
2. Рассмотрим ΔАВК - прямоугольный.
По теореме Пифагора:
АВ² = АК² + ВК²
49 = (7 - х)² + 3х²
49 = 49 - 14х + х² + 3х²
4х² - 14х = 0
2х · (2х - 14) = 0
1) х = 0 - не подходит по условию задачи.
2) 2х - 14 = 0
2х = 14
⇒ BD = 2x = 14 см.
Длина диагонали BD равна 14 см.
Приложения:
kimkarina953:
доброе утро. вы не могли бы мне помочь с геометрией пожалуйста умоляюю
Добрый вечер. Вы не могли бы мне помочь с геометрией пожалуйста
Вас заинтересует
1 год назад
1 год назад
2 года назад
2 года назад
7 лет назад
7 лет назад
8 лет назад
