Допоможіть будь ласка)
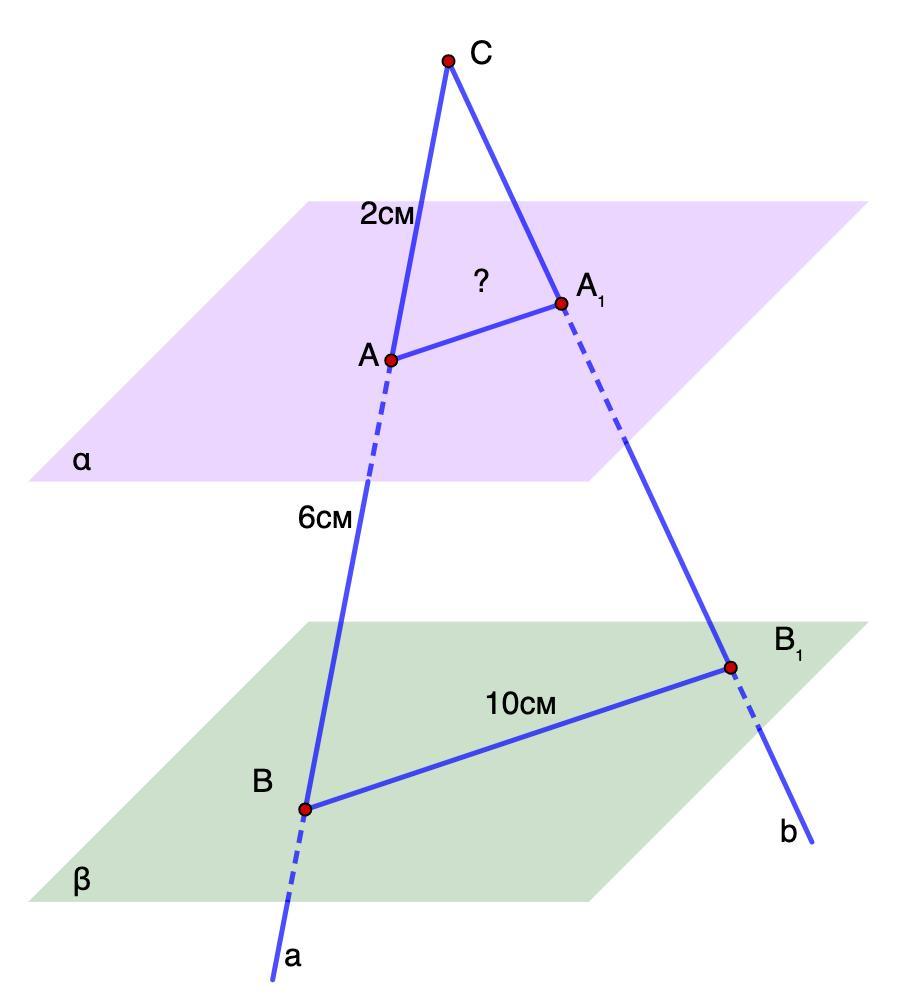
1. Через точку С, яка лежить поза паралельними площинами α і β, проведено прямі a i b, що перетинають площину α в точках А і А1, а площину β у точках В і В1 відповідно
Знайдіть АА1, якщо: АС = 2 см, АВ = 6 см, ВВ1 = 10 см
зробіть на малюнку площіни а ß пряму а і тачку а якщо а(а а(ß а є ß а не є а
Ответы
Ответ дал:
9
Ответ:
Отрезок АА₁ равен 2,5 см.
Объяснение:
Через точку С, которая лежит вне параллельными плоскостями α и β, проведены прямые a и b, пересекающие плоскость α в точках А и А₁, а плоскость β в точках В и В₁ соответственно
Найдите АА₁, если: АС = 2 см, АВ = 6 см, ВВ₁ = 10 см
Дано: α || β;
a ∩ b = C;
a ∩ α = A; a ∩ β = B;
b ∩ α = A₁; b ∩ β = B₁;
АС = 2 см, АВ = 6 см, ВВ₁ = 10 см
Найти: АА₁
Решение:
a ∩ b = C
- Через две пересекающиеся прямые a и b проходит плоскость, и при том только одна.
⇒ a и b принадлежат одной плоскости.
- Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны.
⇒ АА₁ || BB₁
Рассмотрим ΔВСВ₁ и ΔАСА₁.
АА₁ || BB₁.
- Лемма. Если две стороны треугольника пересекает прямая, параллельная третьей стороне, то она отсекает треугольник, подобный данному.
⇒ ΔВСВ₁ ~ ΔАСА₁.
Запишем отношения сходственных сторон:
(см)
Отрезок АА₁ равен 2,5 см.
#SPJ1
Приложения:
Вас заинтересует
2 года назад
2 года назад
2 года назад
7 лет назад
9 лет назад
9 лет назад
6 см
Пояснення:
через дві прямі, що перетинаються, можна провести одну площину.
Побудуємо площину гамма на прямих а і b, яка перетинає площини α та β по прямим АВ та В1А1 відповідно.
З властивості паралельних площин → якщо дві паралельні площини перетнути третьою, то прямі їхнього петину, паралельні → АВ||А1В1