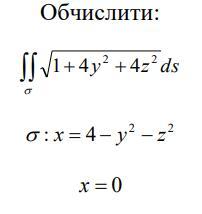Question

Завдання з вищої математики

Answer 1

Ответ:

Поверхностный интеграл:

$\boldsymbol{\boxed{\displaystyle \iint\limits_{\sigma} {\sqrt{1 + 4y^{2} + 4z^{2}} } \, ds = 36 \pi }}$

Примечание:

Если $S \ -$ гладкая поверхность заданная уравнением

$x = \xi(y,z)$

$\sigma \ -$ замкнутая квадратируемая область являющееся проекцией $S$ на плоскость $yz$.

Функция $f(x,y,z)$ - непрерывна на $S$

Тогда:

$\boldsymbol{\boxed{\iint\limits_{S} {f(x,y,z)} \, ds = \iint\limits_{\sigma} {f(\xi(y,z),y,z)\sqrt{1 + \bigg( \frac{\partial \xi}{\partial y} \bigg)^{2} + \bigg( \frac{\partial \xi}{\partial z} \bigg)^{2}} } \, dydz}}$

Пошаговое объяснение:

Необходимо вычислить поверхностный интеграл:

$\displaystyle \iint\limits_{\sigma} {\sqrt{1 + 4y^{2} + 4z^{2}} } \, ds$

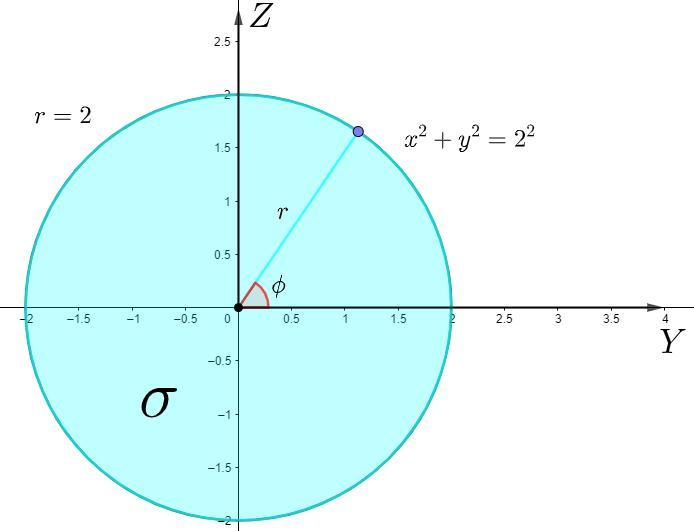
Поверхность $\sigma:$

$x = 4 - y^{2} - z^{2}$

$x = 0$

Проекция $x = 4 - y^{2} - z^{2}$ на плоскость $YZ:$

$4 - y^{2} - z^{2} = 0$

$\sigma :y^{2} + z^{2} = 2^{2}$

Частные производные функции $x = 4 - y^{2} - z^{2}$:

$\dfrac{\partial \xi}{\partial z} = \dfrac{\partial }{\partial z} \bigg(4 - y^{2} - z^{2} \bigg) =-2z$

$\dfrac{\partial \xi}{\partial y} = \dfrac{\partial }{\partial y} \bigg(4 - y^{2} - z^{2} \bigg) =-2y$

----------------------------------------------------------------------

$\displaystyle \iint\limits_{\sigma} {\sqrt{1 + 4y^{2} + 4z^{2}} \sqrt{1 + (-2y)^{2} + (-2z)^{2}} } \, dydz = \iint\limits_{\sigma} {\sqrt{1 + 4y^{2} + 4z^{2}} \sqrt{1 + 4y^{2} + 4z^{2}} } \, dydz =$

$\displaystyle =\iint\limits_{\sigma} {\bigg( 1 + 4y^{2} + 4z^{2} \bigg) } \, dydz ;$

Удобно перейти в полярную систему координат:

$\displaystyle \left \{ {{y = r \cos \phi} \atop {z=r \sin \phi}} \right.$

С помощью Якобиана перехода к полярным координатам получаем:

$dydz = r \ drd\phi$

Уравнение проекции поверхности в полярных координатах:

$\sigma :y^{2} + z^{2} = 2^{2}$

$(r \cos \phi)^{2} + (r \sin \phi)^{2} = 2^{2}$

$r^{2} \cos^{2} \phi + r^{2} \sin^{2} \phi = 4$

$r^{2} ( \cos^{2} \phi + \sin^{2} \phi) = 4$

$r^{2} = 4 \Longrightarrow r = 2$, так как по определению $r > 0$.

Тогда:

$\displaystyle \iint\limits_{G} {f(y,z)} \, dydz = \iint\limits_{G} {f(r \cos \phi,r\sin \phi)}r \, drd\phi$

Следовательно:

$\displaystyle \iint\limits_{\sigma} {\bigg( 1 + 4y^{2} + 4z^{2} \bigg) } \, dydz = \iint\limits_{\sigma} {r\bigg( 1 + 4(r \cos \phi)^{2} + 4(r \sin \phi)^{2} \bigg) } \, drd \phi =$

$\displaystyle = \iint\limits_{\sigma} {r\bigg( 1 + 4r^{2} \cos^{2} \phi + 4r^{2} \sin^{2} \phi \bigg) } \, drd \phi = \iint\limits_{\sigma} {r\bigg( 1 + 4r^{2} (\cos^{2} \phi + } \sin^{2} \phi) \bigg) } \, drd \phi =$

$\displaystyle = \iint\limits_{\sigma} {r\bigg( 1 + 4r^{2} \bigg) } \, drd \phi = \iint\limits_{\sigma} {\bigg( r + 4r^{3} \bigg) } \, drd \phi =$

При интегрировании по окружности полярный радиус будет меняться в промежутке [0;2π] и радиус будет изменяться от нуля до 2 (радиус окружности; см. уравнение $\sigma$ в полярных координатах).

$\displaystyle = \int\limits^{2 \pi}_{0} \, d\phi \int\limits^{2}_{0} {\bigg( r + 4r^{3} \bigg)} \, dr = \int\limits^{2 \pi}_{0} {\Bigg( \bigg(\frac{r^{2}}{2} + r^{4} \bigg) \bigg |_{0}^{2} \Bigg)} \, d\phi =$

$\displaystyle \int\limits^{2 \pi}_{0} {\Bigg( \bigg(\frac{2^{2}}{2} + 2^{4} \bigg) - \bigg(\frac{0^{2}}{2} + 0^{4} \bigg) \Bigg)} \, d\phi = \int\limits^{2 \pi}_{0} {(2 + 16)} \, d\phi = 18\int\limits^{2 \pi}_{0} \, d\phi = 18 \cdot \phi \bigg |_{0}^{2 \pi } =$

$= 18(2 \pi - 0) = 18 \cdot 2\pi = 36 \pi$