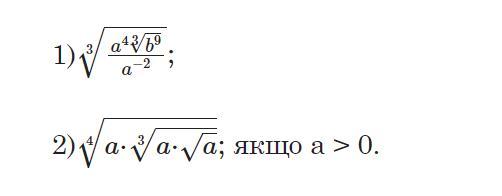Question

На якість будь-ласка. Хочу зрозуміти як вирішувати.

Answer 1

1)

$\sqrt[3]{ \frac{ {a}^{4} \sqrt[3]{ {b}^{9} } }{ {a}^{ - 2} } }$

$\sqrt[3]{ {b}^{9} } = {b}^{ \frac{9}{3} } = {b}^{3}$

При діленні, степені віднімаються

${a}^{4} \div {a}^{ - 2} = {a}^{4 - ( - 2)} = {a}^{4 + 2} = {a}^{6}$

$\sqrt[3]{ {a}^{6} {b}^{3} }$

Виносимо вирази з під кореня, для цього потрібно степінь поділити на корінь степеня

$\sqrt[3]{ {a}^{6} } = {a}^{ \frac{ 6}{3} } = {a}^{2}$

$\sqrt[3]{ {b}^{3} } = {b}^{ \frac{3}{3} } = b$

$\sqrt[3]{ \frac{ {a}^{4} \sqrt[3]{ {b}^{9} } }{ {a}^{ - 2} } } = \sqrt[3]{ {a}^{6} {b}^{3} } = {a}^{2} b$

2)

$\sqrt[4]{a \times \sqrt[3]{a \times \sqrt{a} } }$

За формулою

$a = \sqrt[n]{ {a}^{n} }$

Перетворимо вирази

$\sqrt[4]{ \sqrt{ {a}^{2} } \sqrt[3]{ \sqrt{ {a}^{2} } \sqrt{a} } }$

Вираз коренів з одинковим степенем дорівнює кореню

$\sqrt{ {a}^{2} } \times \sqrt{a} = \sqrt{ {a}^{2} \times a } = \sqrt{ {a}^{2 + 1} } = \sqrt{ {a}^{3} }$

$\sqrt[4]{ \sqrt{ {a}^{2} } \sqrt[3]{ \sqrt{ {a}^{3} } } }$

Спростимо вираз використовуючи формулу

$\sqrt[m]{ \sqrt[n]{a} } = \sqrt[mn]{a}$

$\sqrt[3]{ \sqrt{ {a}^{3} } } = \sqrt[2 \times 3]{ {a}^{3} } = \sqrt[6]{ {a}^{3} }$

$\sqrt[4]{ \sqrt{ {a}^{2} } \sqrt[6]{ {a}^{3} } }$

Скоротимо степень кореню

$\sqrt[6]{ {a}^{3} } = \sqrt[6 \div 3]{a} = \sqrt{a}$

$\sqrt[4]{ \sqrt{ {a}^{2} } \sqrt{a} }$

Користуючись формулами вище, повторимо дії

$\sqrt[4]{ \sqrt{ {a}^{2} \times a} } = \sqrt[4]{ \sqrt{ {a}^{3} } } = \sqrt[4 \times 2]{ {a}^{3} } = \sqrt[8]{ {a}^{3} }$