Question

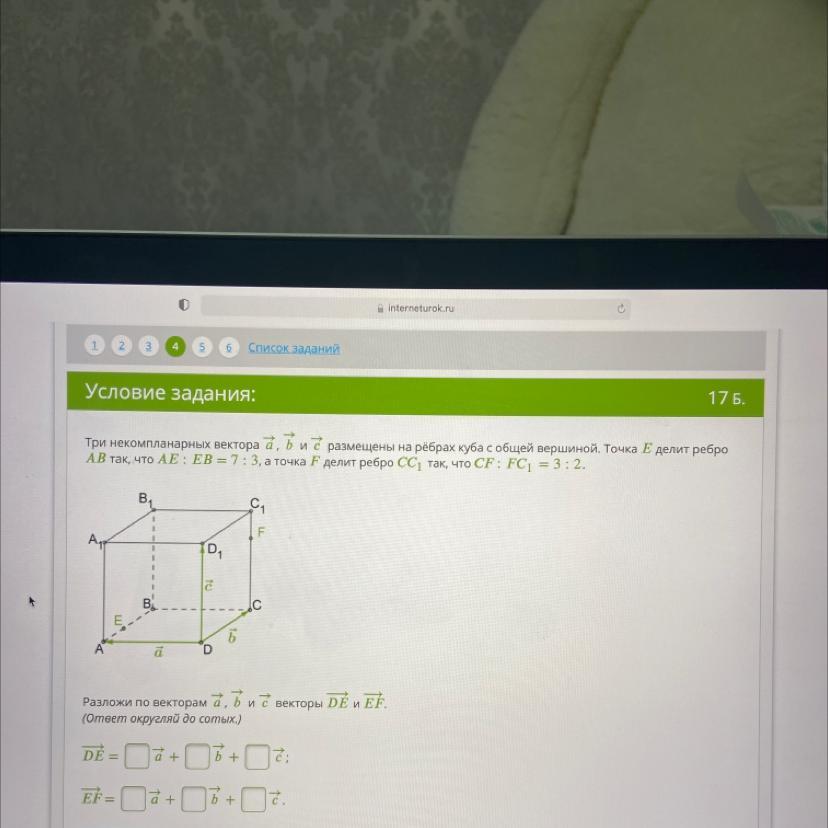
Три некомпланарных вектора а, ь и с размещены на рёбрах куба с общей вершиной. Точка Е делит ребро
А В так, что АЕ : EB = 7: 3, а точка F делит ребро СС так, что CF : FC1 = 3 : 2.

Answer 1

Ответ: пусть куб имеет единичные ребра, тогда некомпланарные векторы можем использовать, как ортонормированный базис, что позволит не использовать матрицу Грамма.

В таком случае, вектор DE может быть выражен как а + 0,3b, а вектор ЕF можно выразить b + 0,6c, или же DE = (1, 0.3, 0) и b = (0, 1, 0.6) в новом базисе

Объяснение: