Это интересно!!!
Уравнение. Найти корни. Опечаток нет. В других вариантов также( в смысле, так просто корни не найдешь. Похоже, нет корней.Тогда как доказать?) В чем заковырка, а? Помогите решить:)
Приложения:
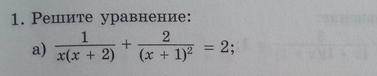
Ответы
Ответ дал:
0
открываем скобки и переносим все в одну сторону:
Собираем все под общий знаменатель (все писать не буду, даю сразу приведенный результат):
Рассматриваем знаменатель:
X^2 + 2x = 0,
x=0 и х=-2;
x^2+2x+1,
х=-1.
Однако корнями уравнения эти корни являться не могут, так как знаменатель не может равняться нулю. Это выпадающие точки.
Рассматриваем числитель:
2x^4+8x^3+7x^2-2x-1 = 0,
Используем метод неопределенных коэффициентов (удобен тем, что утверждает, что любой многочлен четвертой степени разлагается на произведение многочленов второй степени). Коэффициенты просто угадываются (подбираются).
Получается:
(х^2+2x-1)*(2x^2+4x+1) = 0.
Корни квадратных уравнений находятся просто по дискриминанту:
х^2+2x-1 =0
Х(1) =
Х(2) =
2x^2+4x+1 = 0
х(1) =
х(2) =
Ответ дал:
0
Подбор объяснить не смогу. Он зависит от степени просветления и опыта. ))))
Ответ дал:
0
Спасибо огромное!!!!
Вас заинтересует
2 года назад
2 года назад
8 лет назад
10 лет назад
10 лет назад
11 лет назад