Question

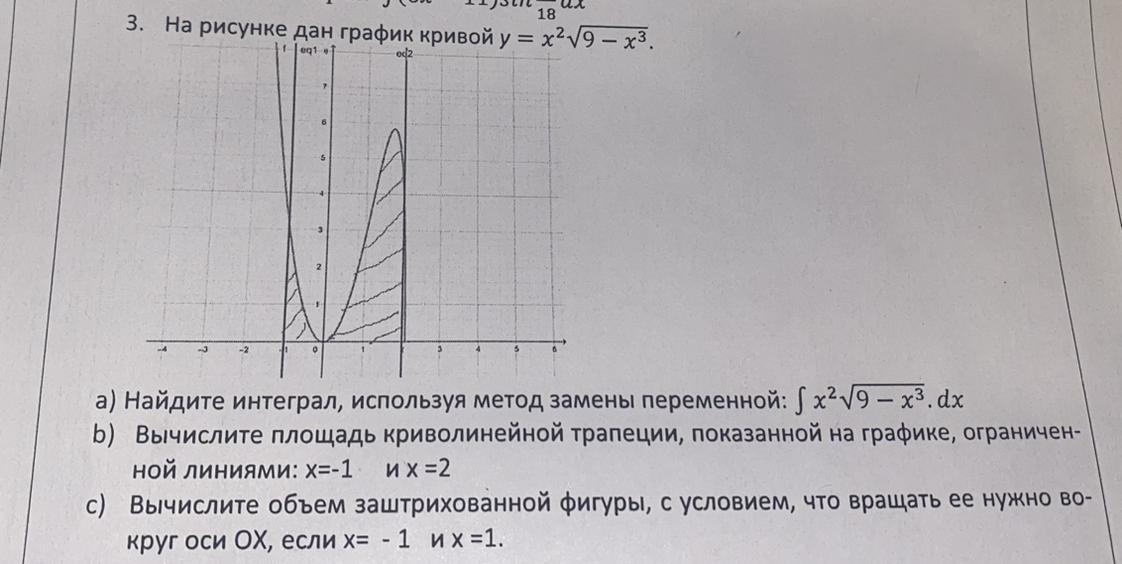
прошу помогите!!! На рисунке дан график кривой у = х^2sqrt(9 - х^3).

a) Найдите интеграл, используя метод замены переменной
b) Вычислите площадь криволинейной трапеции, показанной на графике, ограничен-ной линиями: x=-1 И X =2
с) Вычислите объем заштрихованной фигуры, с условием, что вращать ее нужно во-
круг оси ОХ, если x= - 1 их =1.

Answer 1

Ответ:

$a) ~\displaystyle \int\limits x^2 \sqrt{9-x^3} \, dx =-\frac{2\cdot \sqrt{9-x^3} \cdot (9-x^3)}{9}+C$

$b) ~ S=\dfrac{20\sqrt{10}-2 }{9}\\\\ c) ~ V = 3,6\pi$

Объяснение:

a) Найдите интеграл, используя метод замены переменной

$\displaystyle \int\limits x^2 \sqrt{9-x^3} \, dx = \int\limits x^2 \sqrt{9-x^3}\cdot \frac{1}{(9-x^3)'} \, d(9-x^3) =\\\\\\ =\int\limits x^2 \sqrt{9-x^3} \cdot \frac{1}{-3x^2} \, d(9-x^3) =-\frac{1}{3} \int\limits \sqrt{9-x^3} \, d(9-x^3)$

Вводим замену :

$t=9-x^3$

$\displaystyle -\frac{1}{3} \int\limits \sqrt{t} \, dt = -\frac{1}{3}\cdot \frac{t^{\tfrac{1}{2} +1}}{\tfrac{1}{2}+1 } =-\frac{1}{3} \cdot \frac{2t\sqrt{t} }{3} =-\frac{2}{9}\cdot t\sqrt{t}$

Вернемся к старым переменным :

$\displaystyle -\frac{2}{9}\cdot t\sqrt{t} =-\frac{2\cdot \sqrt{9-x^3} \cdot (9-x^3)}{9}+C$

b) Вычислите площадь криволинейной трапеции, показанной на графике, ограничен-ной линиями: x=-1 и x=2

Сначала найдем площадь фигуры которая ограничена линиями           x = 0 ,   x = -1

$S_1 = \displaystyle \int\limits ^0 _{-1} x^2 \sqrt{9-x^3} \, dx =-\frac{2\cdot \sqrt{9-x^3} \cdot (9-x^3)}{9} ~ \Bigg |^0_{-1} = \\\\= -\frac{2\cdot 3 \cdot 9}{9} - \bigg ( -\frac{2\cdot \sqrt{10}\cdot 10}{9} \bigg ) =\frac{20\sqrt{10} }{9} - 6$

Теперь найдем площадь фигуры которая ограничена линиями :

$S_2 = \displaystyle \int\limits ^{2}_0 x^2 \sqrt{9-x^3} \, dx=-\frac{2\cdot \sqrt{9-x^3} \cdot (9-x^3)}{9} ~ \Bigg |^2_{0} =-\frac{2\sqrt{9-8}(9-8) }{9} + 6 =\\\\=- \frac{2}{9} + 6$

Находим площадь всей нашей фигуры :

$S=S_1 + S_2 = \dfrac{20\sqrt{10} }{9}- 6 +6-\dfrac{2}{9} = \dfrac{20\sqrt{10}-2 }{9}$

с) Вычислите объем заштрихованной фигуры, с условием, что вращать ее нужно во-круг оси ОХ, если x= - 1 их =1.

Формула для нахождения объема при вращении тела :

$\displaystyle \boldsymbol{V = \pi \cdot \int\limits^a_b {f^2(x)} \, dx }$

Таким же образом  как и в  b) сначала найдем объем фигуры которая ограничена  линиями   x = - 1  ,  x =0  

$\displaystyle V_1 = \pi \cdot \int\limits ^0_{-1} ( x^2 \sqrt{9-x^3})^2 \, dx = \pi\cdot \int\limits^0_{-1}x^4 \cdot (9-x^3) \, dx =\pi \int\limits^0_{-1}( 9x^4 - x^7 )\, dx = \\\\\\ =\pi \bigg (9 \cdot \frac{x^5}{5} -\frac{x^8}{8} \bigg) \Bigg |^0_{-1} =\pi \bigg (0 -\bigg ( -\frac{9}{5} -\frac{1}{8} \bigg ) \bigg )= 1,925 \pi$

Теперь найдем объем фигуры которая ограничена линиями

x = 1  ,   x = 0

$\displaystyle V_2 = \pi \cdot \int\limits ^1_{0} ( x^2 \sqrt{9-x^3})^2 \, dx = \pi\cdot \int\limits^1_{0}x^4 \cdot (9-x^3) \, dx =\pi \int\limits^1_{0}( 9x^4 - x^7 )\, dx = \\\\\\ =\pi \bigg (9 \cdot \frac{x^5}{5} -\frac{x^8}{8} \bigg) \Bigg |^1_{0} =\pi \bigg ( \frac{9}{5} -\frac{1}{8} + 0 \bigg )= 1,675 \pi$

Соответственно объем всей фигуры равен :

$V = V_1 + V_2 = 1,925 \pi + 1,675\pi = 3,6\pi$

#SPJ1