В параллелограмме EFKL диагонали пересекаются в точке О. Докажите, что четырехугольник
ABCD, вершинами которого являются середины отрезков OE, OF. OK и OL - параллелограмм.
Ответы
Ответ дал:
0
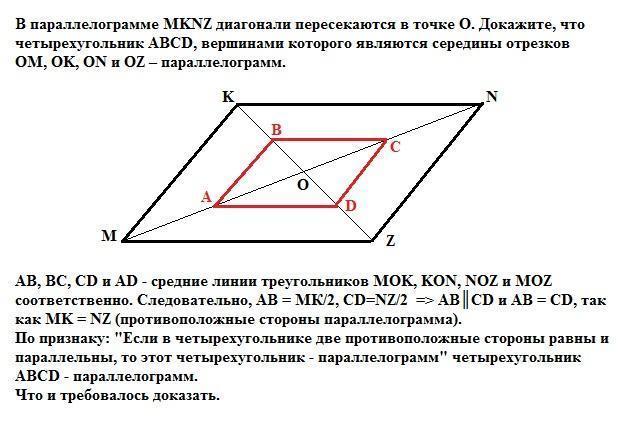
АВ, ВС, CD и AD - средние линии треугольников MOK, KON, NOZ и MOZ соответственно. Следовательно, АВ = МК/2, CD=NZ/2 =>
АВ║CD и AB = CD, так как MK = NZ (противоположные стороны параллелограмма).
По признаку: "Если в четырехугольнике две противоположные стороны равны и параллельны, то этот четырехугольник - параллелограмм" четырехугольник АВСD - параллелограмм.
Что и требовалось доказать.
чел подставь вместо моих свои
Приложения:
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
7 лет назад
7 лет назад