Question

Геометрия даю 100 баллов!​

Answer 1

Ответ:

Угол между диагоналями прямоугольника равен 45°.

Объяснение:

5.Серединный перпендикуляр, проведенный к диагонали прямоугольника, делит большую сторону прямоугольника на части, одна из которых равна меньшей стороне прямоугольника. Найти угол между диагоналями прямоугольника.

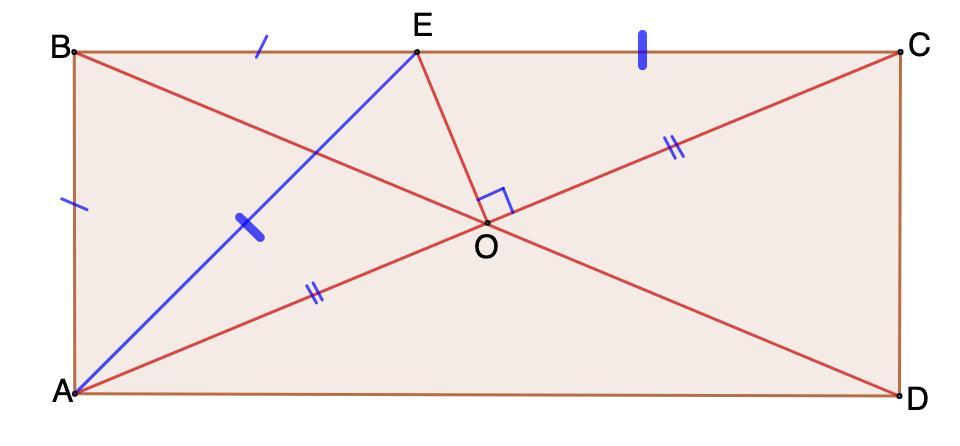
Дано: ABCD - прямоугольник;

АС и ВD - диагонали;

ОЕ - серединный перпендикуляр;

ВЕ = АВ.

Найти: ∠ВОА.

Решение:

Соединим точки А и Е.

1. Рассмотрим ΔАВЕ.

ВЕ = АВ (условие)

⇒ ΔАВЕ - равнобедренный.

• Углы при основании равнобедренного треугольника равны.

• Сумма острых углов прямоугольного треугольника равна 90°.

⇒ ∠АВЕ = ∠ВАЕ = 90° : 2 = 45°

2. Рассмотрим ΔАЕС.

ОЕ ⊥ АС, АО = ОС (условие)

• Если в треугольнике высота является медианой, то этот треугольник равнобедренный.

⇒ ∠ЕАС = ∠ЕСА

• Сумма смежных углов равна 180°.

⇒ ∠АЕС = 180° - ∠АЕВ = 180° - 45° = 135°

ЕАС = ∠ЕСА = (180° - 135°) : 2 = 22,5°

3. Рассмотрим ΔАВО.

• Диагонали прямоугольника равны и точкой пересечения делятся пополам.

⇒ ВО = ОА

ΔАВО - равнобедренный.

∠ВАО = ∠АВО = 45° + 22,5° = 67,5°

⇒ ∠ВОА = 180° - (67,5° + 67,5°) = 45°

Угол между диагоналями прямоугольника равен 45°.

Answer 2

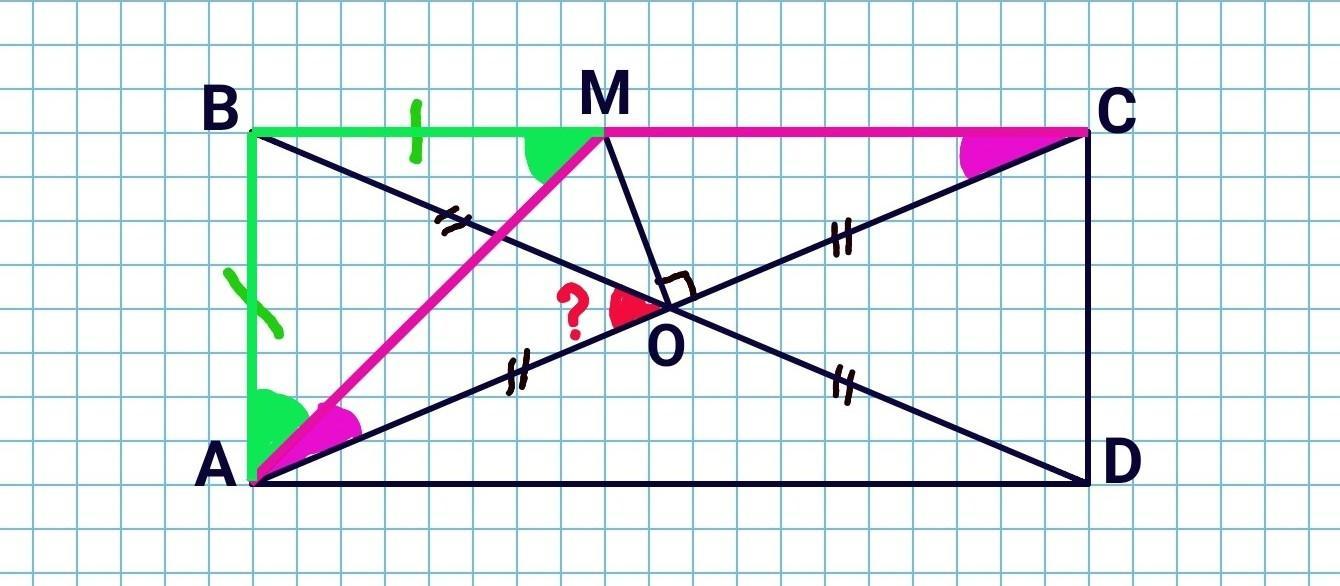
Ответ:

Угол между диагоналями равен 45°

Объяснение:

• Прямоугольник - это параллелограмм, у которого все углы прямые.
• Диагонали прямоугольника точкой пересечения делятся пополам.

ДАНО: ABCD - прямоугольник, МО - серединный перпендикуляр (то есть перпендикуляр, проведенный к середине) к диагонали АС. МО⟂АС, АО=ОС.

Точка М ∈ ВС, АВ=ВМ.

НАЙТИ: ∠АОВ.

РЕШЕНИЕ

1) Рассмотрим прямоугольный треугольник АВМ(∠В=90°).

АВ=МВ - по условию, значит треугольник равнобедренный с основанием АМ.

Известно, что сумма острых углов прямоугольного треугольника равна 90°, поэтому:

∠ВАМ=∠ВМА=90°:2=45° - как углы при основании равнобедренного треугольника.

2) Рассмотрим треугольник АМС.

МО⟂АС, ⇒ МО - высота △АМС.

АО=ОС, ⇒ МО - медиана △АМС.

• Если в треугольнике высота совпадает с медианой, то такой треугольник - равнобедренный.

⇒△АМС - равнобедренный с основанием АС.

∠ВМА - внешний угол для △АМС.

• Внешний угол треугольника равен сумме двух других углов треугольника, не смежных с ним.

Поэтому ∠ВМА=∠МАО+∠МСО, но ∠МАО=∠МСО - как углы при основании равнобедренного треугольника, следовательно ∠ВМА=2•∠МАО,

∠МАО=∠ВМА:2=45°:2= 22,5°

3) Рассмотрим треугольник АОВ.

АО=ВО - как диагонали прямоугольника, следовательно треугольник АОВ - равнобедренный с основанием АВ. Следовательно:

∠ОВА=∠ОАВ=∠ВАМ+∠МАО=45°+22,5°= 67,5°

4) Находим угол между диагоналями прямоугольника:

∠АОВ=180°-∠ОВА-∠ОАВ=180°-67,5°-67,5°=180°-135°= 45°

ОТВЕТ: ∠АОВ=45°