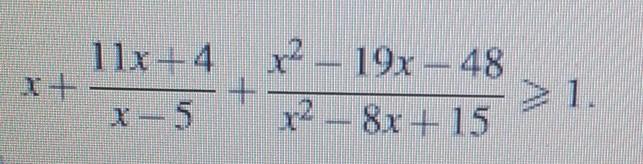Question

пожалуйста объясните как это решать ​

Answer 1

Ответ:

$\{-3\}\cup (5;+\infty)$

Пошаговое объяснение:

Если делать по стандартной схеме - всё перенести налево, привести к общему знаменателю, после чего раскладывать числитель и знаменатель на множители, -  вычисления будут не самые приятные. Данный конкретный пример можно решить проще, если предварительно разложить числитель и знаменатель второй дроби на множители и сократить общий множитель:

        $x+\dfrac{11x+4}{x-5}+\dfrac{(x-3)(x-16)}{(x-3)(x-5)}\ge 1;\ x+\dfrac{11x+4}{x-5}+\dfrac{x-16}{x-5}-1\ge 0.$

Чтобы не забыть, ищем сейчас ОДЗ (не забывая, что сокращали на  

(x-3)):                                   x≠3;    x≠5.

Приводим к общему знаменателю:

    $\dfrac{x^2-5x+11x+4+x-16-x+5}{x-5}\ge 0;\ \dfrac{x^2+6x+9}{x-5}\ge 0;\ \dfrac{(x+3)^2}{x-5}\ge 0.$

Далее или применяем стандартный метод интервалов, или решаем совсем просто: числитель равен нулю  при x= - 3 (минус три поэтому включаем в ответ), а при остальных  x он больше нуля, поэтому не влияет на знак дроби. Следовательно знаменатель должен быть больше нуля. Поэтому ответ такой:

                                     $x\in \{-3\}\cup (5;+\infty).$

Конечно, одним глазом проверяем, не влияет ли ОДЗ на полученный ответ, и видим, что не влияет.