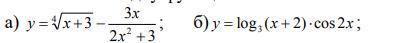Ответы
Ответ дал:
0
Ответ:
Производные функций:
а)
б)
Примечание:
По таблице производных:
, где
Правила дифференцирования:
, где
функции одной переменной
Пошаговое объяснение:
а)
б)
Вас заинтересует
1 год назад
1 год назад
1 год назад
1 год назад
3 года назад
3 года назад
8 лет назад
8 лет назад