Question

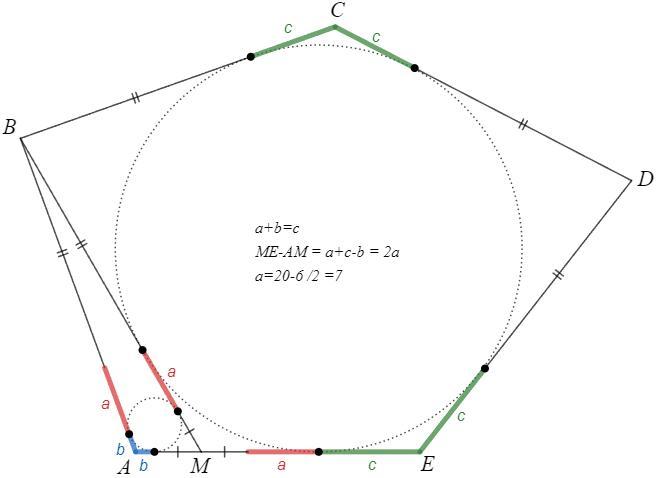
В пятиугольнике ABCDE стороны AB, BC, CD, DE равны. На стороне AE взята точка M так, что AM = 6.0, ME = 20.0. В треугольник ABM и пятиугольник MBCDE вписаны окружности. Найти расстояние между точками касания этих окружностей с отрезком BM. Запишите точный ответ в виде десятичной дроби.

Answer 1

Ответ:

a =(20-6)/2 =7

Объяснение:

Отрезки касательных из одной точки равны.

Решение на картинке.