Ответы
Дана функция у = -х³-3х
1) Область определения функции. Так как функция не имеет дроби или корня, то нет ограничения в области её определения.
D(y) = (−∞; +∞).
2) Четность и нечетность функции:
Проверим функцию - четна или нечетна с помощью соотношений f(x)=f(-x) и f(x)=-f(x). Итак, проверяем: f(-x)=〖-(-x)〗^3-3*(-x)=x^3+3x≠f(x)≠-f(x).
3начит, функция не является ни чётной, ни нечётной.
3) Определим точки пересечения графика функции с осями координат.
Найдем точки пересечения с осью ординат Oy, для чего приравниваем x = 0: у = -03 – 3*0 = 0.
Таким образом, точка пересечения с осью Oy имеет координаты (0; 0).
Найдем точки пересечения с осью абсцисс Ox, для чего надо решить кубическое уравнение x3 – 3x = 0.
Разложим на множители: -x3 – 3x = -x(x² +3) = 0.
Видим, что имеем один корень х = 0, так как второй множитель не может быть равным 0.
Таким образом, точка пересечения с осью Oх имеет координаты (0; 0).
4) Стационарные точки , интервалы возрастания и убывания функции , экстремумы функции
Исследуем функцию на экстремумы и монотонность. Для этого найдем первую производную функции: y’ = (-x3 – 3x )’ = -3x2 – 3 = -3(x2 + 1).
Приравняем первую производную к нулю и найдем стационарные точки (в которых y′=0: -3(x2 + 1) = 0.
Нет критических точки, так выражение не может равным нулю.
Поэтому функция не имеет экстремумов.
При x ∈ (-∞; ∞) производная положительна y′ > 0, функция возрастает на всей области определения и нет точек перегибов графика функции:
6) Дополнительные точки для построения графика функции y(x) = -x3 − 3x:
x y
-3 36
-2,5 23,125
-2 14
-1,5 7,875
-1 4
-0,5 1,625
0 0
0,5 -1,625
1 -4
1,5 -7,875
2 -14
2,5 -23,125
3 -36
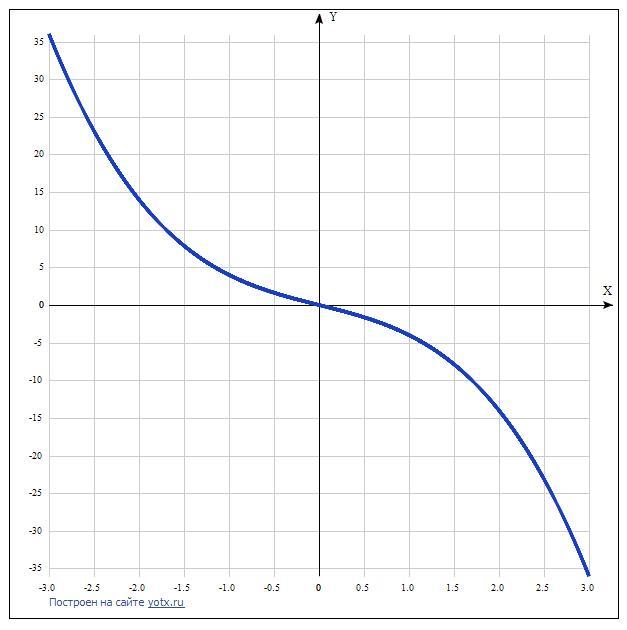
6) По полученным данным строим график, и отметим характерные точки (пересечения с осями).