Ответы
Ответ дал:
0
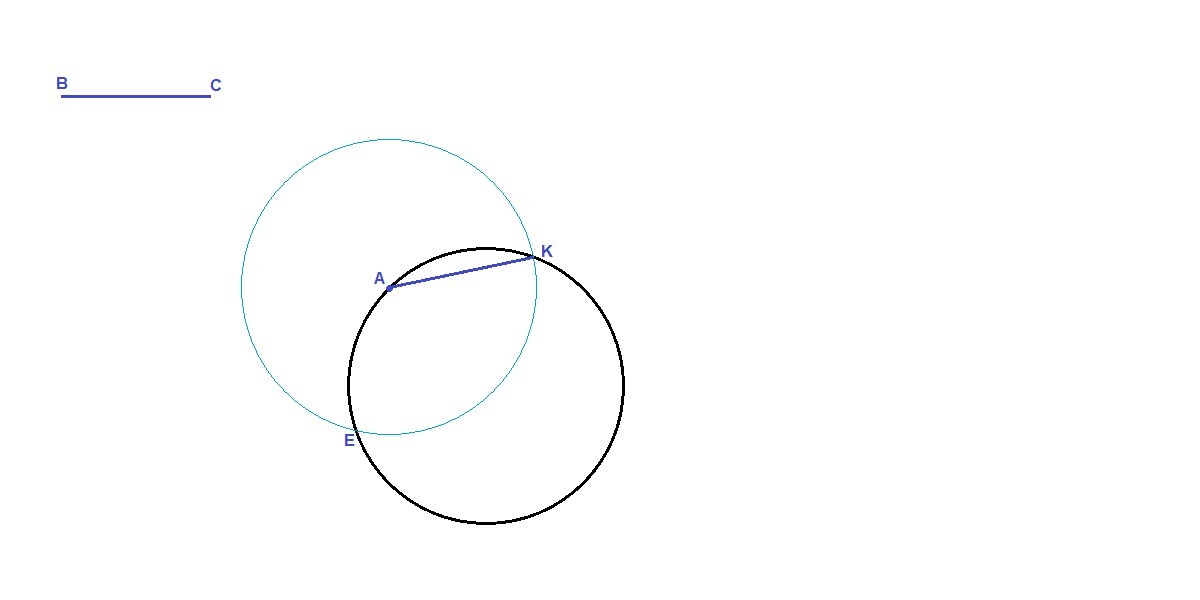
Отметим на окружности произвольную точку А.
Проведем окружность с центром в точке А и радиусом, равны длине данного отрезка ВС.
Точки пересечения этой окружности с данной - Е и К.
Соединим любую из этих точек с точкой А.
АК - искомая хорда.
Доказательство:
АК = ВС, так как это радиус вспомогательной окружности.
Задача имеет решение, если длина данного отрезка не превышает диаметр данной окружности.
Приложения:
Вас заинтересует
2 года назад
2 года назад
8 лет назад
8 лет назад
10 лет назад
10 лет назад
10 лет назад