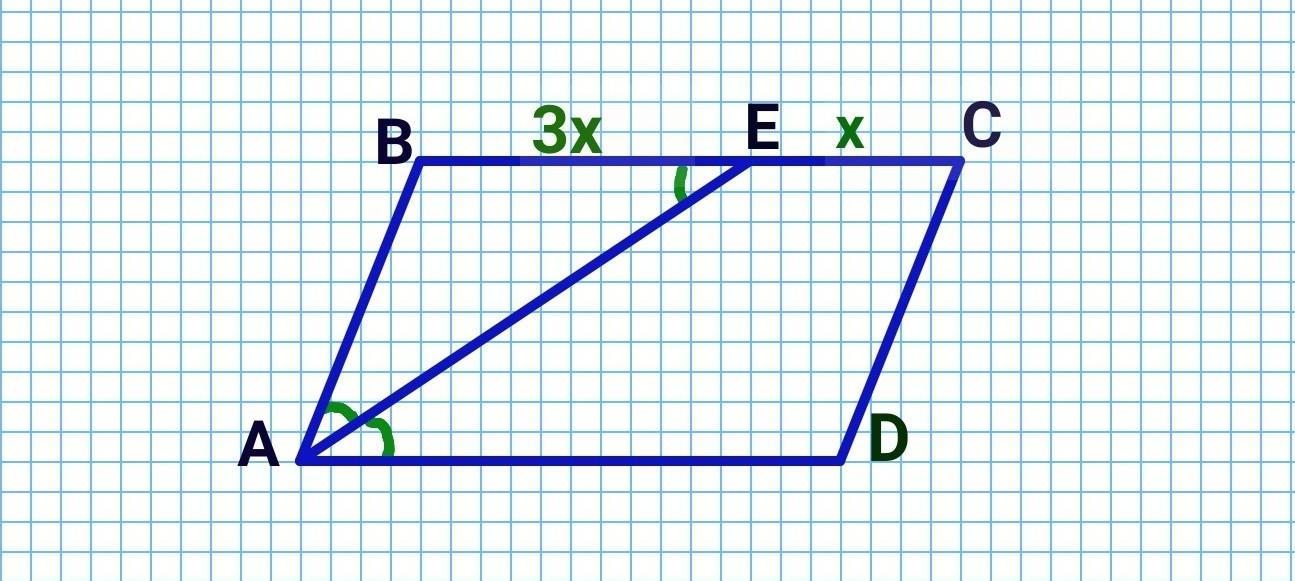
4. В параллелограмме ABCD биссектриса угла А пересекает сторо- ну ВС в точке Е. Отрезок ВЕ больше отрезка ЕС в 3 раза. Найдите периметр параллелограмма, если ВС = 12 см.
Ответы
Ответ:
Периметр параллелограмма равен 42 см
Объяснение:
В параллелограмме ABCD биссектриса угла А пересекает сторону ВС в точке Е. Отрезок ВЕ больше отрезка ЕС в 3 раза. Найдите периметр параллелограмма, если ВС = 12 см.
- Параллелограмм - это четырехугольник у которого противоположные стороны попарно параллельны и равны.
- Периметр параллелограмма: P=2(AB+BC)
Дано: АВСD - параллелограмм, АЕ - биссектриса, AE∩BC=E. ∠BAE=∠DAE, BE>EC в 3 раза, ВС=12 см.
Найти: Р(ABCD).
РЕШЕНИЕ
1) Пусть ЕС=x, тогда ВЕ=3x. Так как по условию ВС=12 см, составляем уравнение:
BE+EC=12
х+3х=12
4x=12
x=3
EC=3(см) BE=3•3=9 (см)
2) ∠ BEA=∠DAE - как внутренние накрест лежащие углы при пересечении параллельных прямых AD и BC секущей АЕ.
∠DAE =∠BAE - по условию (свойство биссектрисы), поэтому ∠BEA=∠BAE.
Поэтому, по признаку равнобедренного треугольника: △АВЕ - равнобедренный, с основанием АЕ.
⇒ АВ=ВЕ= 9 (см) - как боковые стороны равнобедренного треугольника.
3) Находим периметр:
P(ABCD)=2(9+12)=2•21= 42 (см)