Question

знайдіть гострий кут ромба якщо його сторона утворює з діагоналями кути один з яких на 28 градусів менший за другий

Answer 1

Ответ:

Гострий кут ромба дорівнює 62°.

Объяснение:

Знайдіть гострий кут ромба, якщо його сторона утворює з діагоналями кути один з яких на 28 градусів менший за другий.

Ромб - це паралелограм, у якого всі сторони рівні.

Властивості ромба:

• діагоналі ромба взаємно перпендикулярні
• діагоналі ромба ділять кути ромба навпіл
• сума будь-яких двох сусідніх кутів ромба дорівнює 180°.

Розв'язання

1.

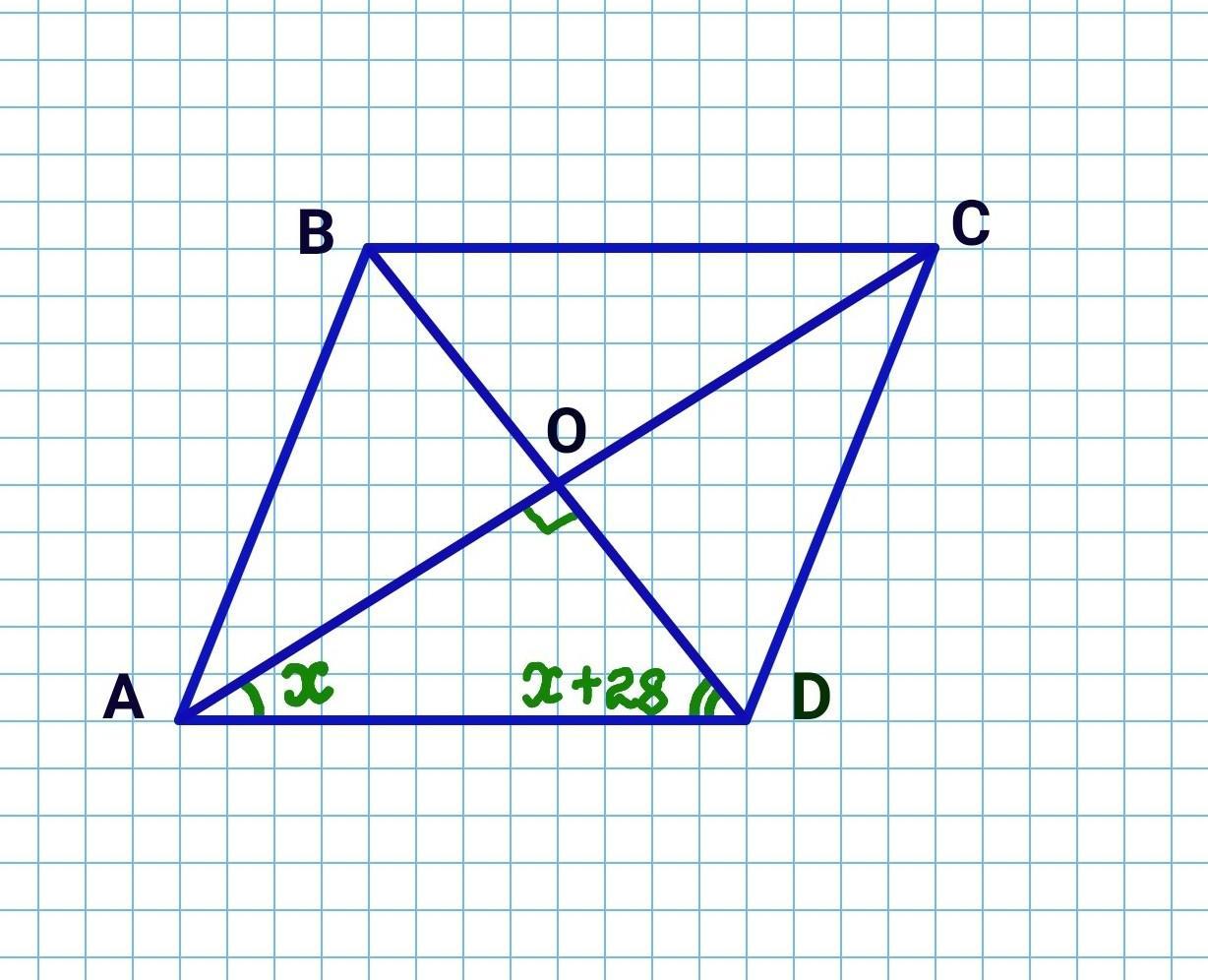
Дан ромб ABCD. Нехай ∠OAD=х°, тоді згідно умови ∠ODA=(x+28)°.

Так як AC⟂BD (властивість ромба), то △АОD - прямокутний.

Сума гострих кутів прямокутного трикутника дорівнює 90°, тому:

х+х+28=90

2х=62

х=31

∠OAD=31°

2.

∠BAD=2•∠BAD=2•31°= 62°(так як АС - бісектриса ∠А)

3.

62°<90° ⇒∠BAD - гострий

Отже, гострий кут ромба дорівнює 62°.