Даю 100 баллов
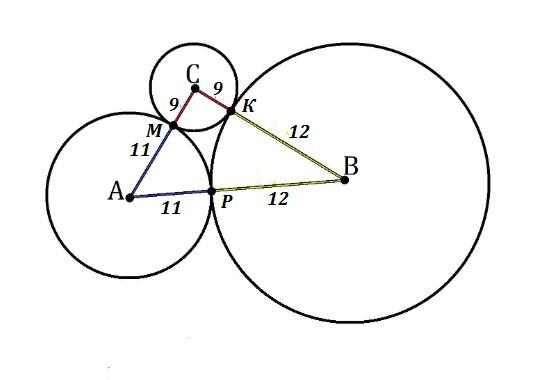
Три кола, радіуси яких 9см, 11см, 12см, попарно дотикаються одне до одного. Визначте площу трикутника, вершинами якого є центри цих кіл.
Ответы
Ответ дал:
0
Решение.
Радиусы окружностей, попарно касающихся друг друга, равны
9 см , 11 см , 12 см .
Центры двух окружностей, касающихся друг друга , и точка их касаниях лежат на одной прямой , поэтому стороны ΔABC , c вершинами в центрах этих окружностей, равны сумме радиусов:
АС=АМ+МС=11+9=20 см , АВ=АР+РВ=11+12=23 см ,
ВС=ВК+КС=12+9=21 см .
Площадь треугольника можно найти по формуле Герона .
.
(см²)
Приложения:
Вас заинтересует
1 год назад
1 год назад
1 год назад
3 года назад
8 лет назад