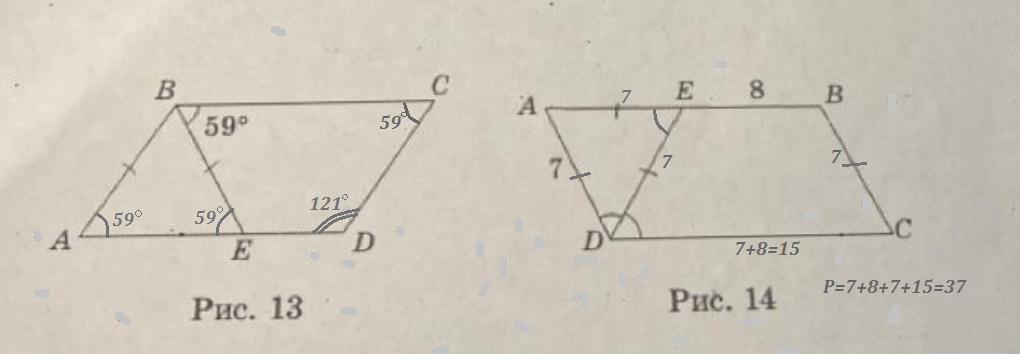Ответы
Ответ:
1) Так как ∠СВЕ и ∠ВЕА - внутренние накрест лежащие углы при ВС||AD (противоположные стороны параллелограмма параллельны) и секущей ВЕ , то ∠СВЕ = ∠ВЕА =59°.
Так как ΔАВЕ - равнобедренный , то ∠ВЕА=∠ВАЕ=59° .
Так как сумма углов параллелограмма , прилежащих к одной его стороне, равна 180° , то ∠АВС=180°-∠ВАЕ=180°-59°=121° .
Но ∠АВС= ∠АDC=121° .
Ответ: углы параллелограмма равны 59°, 121° , 59° , 121° .
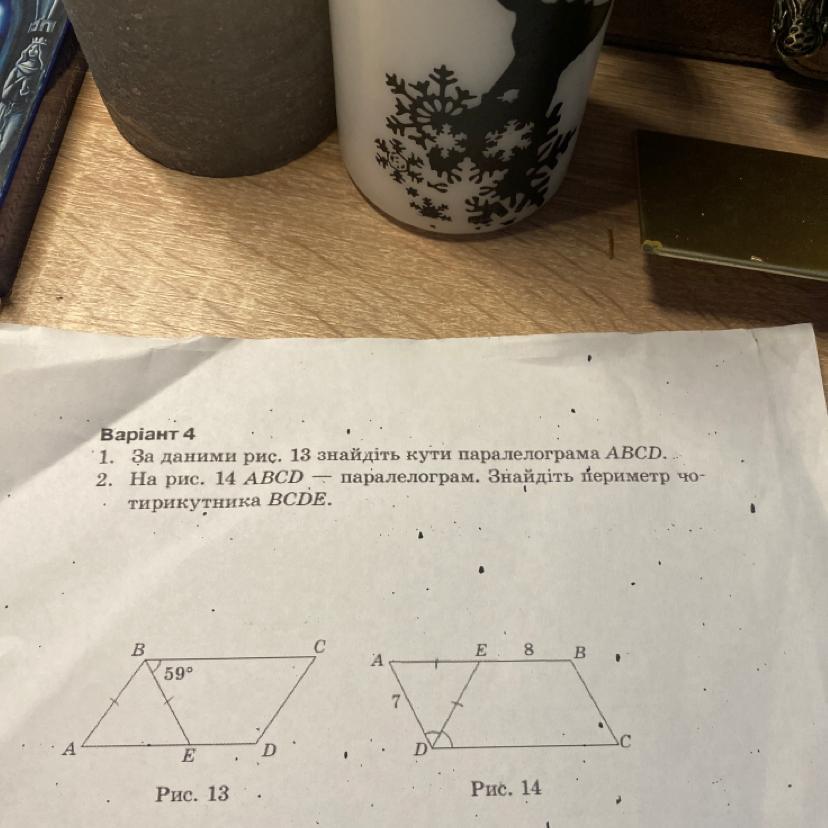
2) Так как DE - биссектриса ∠АDC , то ∠АDЕ=∠ЕDC .
Так как ∠АDЕ и ∠ЕDС - внутренние накрест лежащие углы при АВ||DС (противоположные стороны параллелограмма параллельны) и секущей DЕ , то ∠ЕDC = ∠АЕD .
Тогда ΔАЕD - равнобедренный и АD=АЕ=7 .
DE=АЕ=7 по условию ( тогда ΔАЕD равносторонний )
АВ=АЕ+ЕВ=7+8=15 . Но АВ=СD=15
ВC=АD=7 как противоположные стороны параллелограмма
Периметр четырёхугольника BCDE равен Р=7+8+7+15=37 .