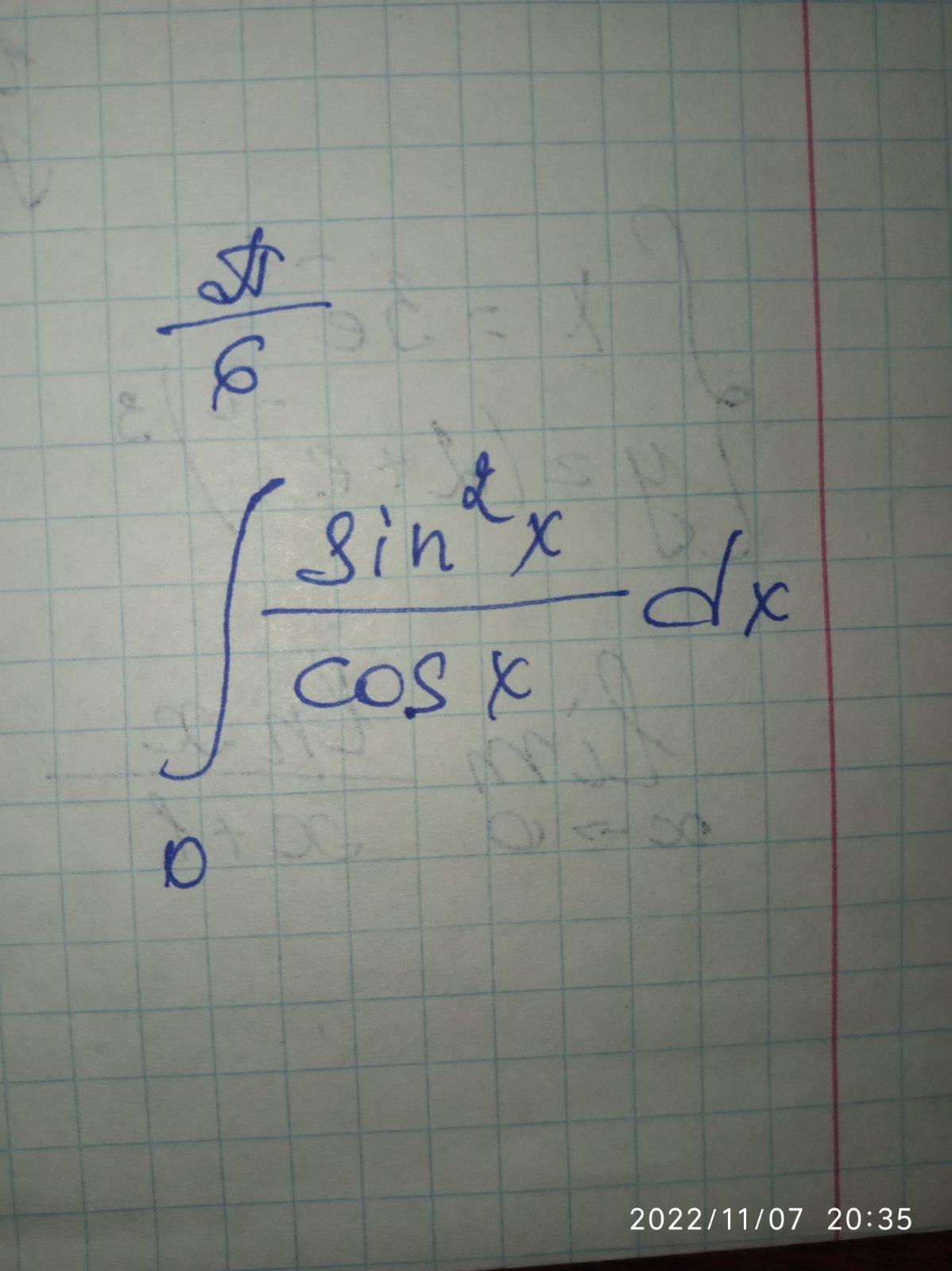Ответы
Ответ дал:
0
Ответ:
∫sec x sin² x dx = 0.05
Пошаговое объяснение:
упростим:
∫sec x sin² x dx Применим линейность: =∫ sec x dx –∫cos x dx Теперь вычисляем: = ∫sec x dx=ln(tan x+sec x) Теперь вычисляем: ∫cos x dx= sin x
Применение модуля к аргументу логарифма, расширяет его диапазон: ln(|tan x+sec x|)- sin x+C
∫sec x sin² x dx = ln(|sin x+1|)/2- ln(1- sin x)/2- sin x+C
∫sec x sin² x dx = ln(|sin π/6+1|)/2- ln(1- sin π/6)/2- sin π/6 =0.05
makar14062014:
дякую
Вас заинтересует
1 год назад
1 год назад
1 год назад
3 года назад
8 лет назад
8 лет назад