Question

1. На сторонах кута в відкладені відрізки BC = 5cM CD = 4CM BE = 6cM EF = 8 см (рис. 8). Знайдіть вiдно

шення площ трикутника ВСЕ і чотирикутника CDFE.

Answer 1

Ответ:

Sbce/Scdfe = 15x/62x = 5/16.

Объяснение:

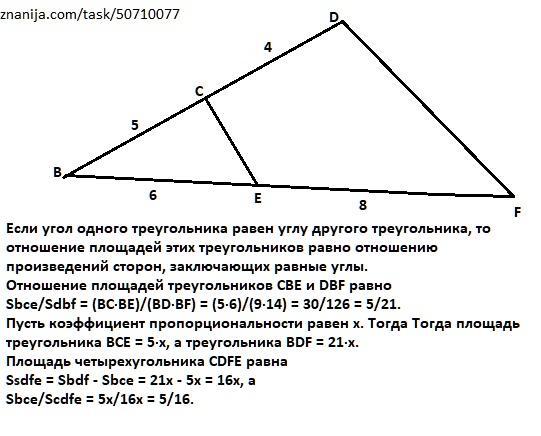
Если угол одного треугольника равен углу другого треугольника, то отношение площадей этих треугольников равно отношению произведений сторон, заключающих равные углы.

Отношение площадей треугольников СВЕ и DBF равно

Sbce/Sdbf = (BC·BE)/(BD·BF) = (5·6)/(9·14) = 30/126 = 5/21.

Пусть коэффициент пропорциональности равен х. Тогда Тогда площадь треугольника ВСЕ = 5·х, а треугольника BDF = 21·х.

Площадь четырехугольника CDFE равна

Ssdfe = Sbdf - Sbce = 21x - 5x = 16x, а

Sbce/Scdfe = 5x/16x = 5/16.