Условие
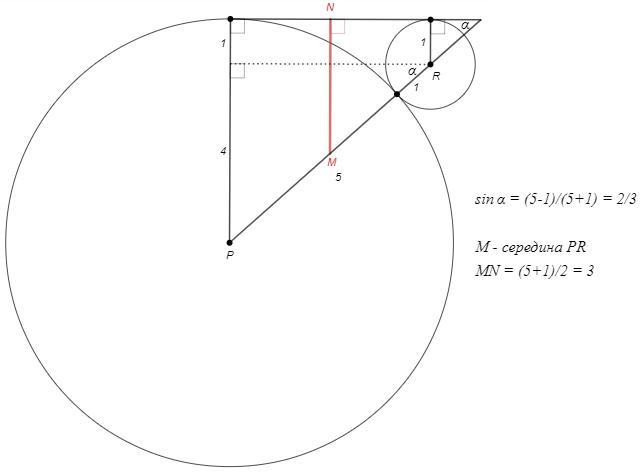
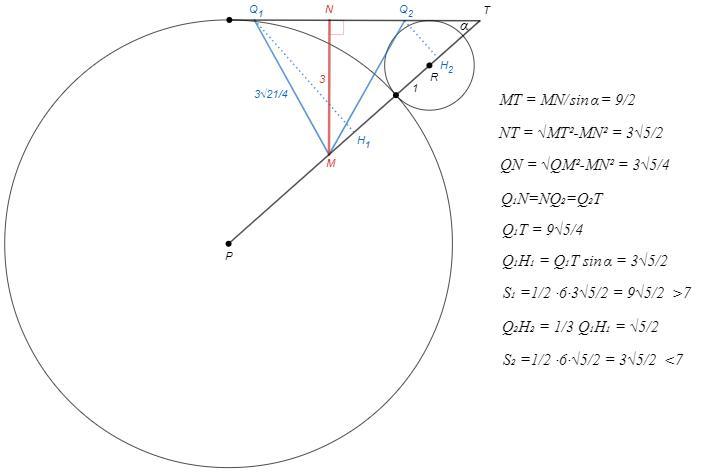
В треугольнике PQR медиана, проведённая из вершины Q, 3√21÷4.Окружности с центрами в вершинах P и R и радиусами соответственно 5 и 1 касаются друг друга, а вершина Q лежит на прямой, касающейся каждой из окружностей. Найдите площадь S треугольника PQR, если известно, что S < 7.

Ответы

Ответ дал: siestarjoki

Ответ:

S=3√5/2

///////////////////////////////////////////////////////////////////////////////

Приложения:

ГАЗ52: А где на 1 чертеже точка ку?

ГАЗ52: Не могу понять почему

siestarjoki: на первом рисунке нет Q

ГАЗ52: А почему Вы её не поставили? Ведь не ясно почему решение пошло по этому пути. Это важно. Без этого долго нужно долго разбираться ( как например я)

siestarjoki: Надо еще рассмотреть внутренне касающиеся окружности и внутреннюю общую касательную и отбросить эти случаи. Останется случай внешнего касания окружностей и внешней общей касательной, на которой две точки Q. Требуется найти QH=QTsina. Из конфигурации с окружностями находим sina, MN и NT. По т Пифагора находим QN. QT=NT+-QN.

ГАЗ52: Ого.

Вас заинтересует

Информатика

1 год назад

СРОЧНО Үй тапсырмасы Зерттеу тақырыптары: Қағазға басу құралдарының даму тарихы Мен және интернет USB құрыл- Ғысы және оның дамуы «Компьютер сәулеті» дегенiмiз не? AHAXNATIX . • . . . . . . Зерттеу

Русский язык

1 год назад

Трактористы² 2 это разобрать по составу типо корень ,суффикс ,окончание,предлог. и основа помогите

История

1 год назад

Задание 2. Проранжируйте причины образования Казахского ханства по степени значимости: (6 б) 1. Стремление султанов Kepeй и Жанибека к образованию независимого государства; 2. Усиление

Алгебра