Докажите , что можно разрезать правильный пятиугольник на 4 части , из которых без просветов и наложений составляется прямоугольник .

Ответы

Ответ дал: siestarjoki

.............................................................................

Приложения:

reygen: А можно немного пояснений , такое доказательство нет примут (

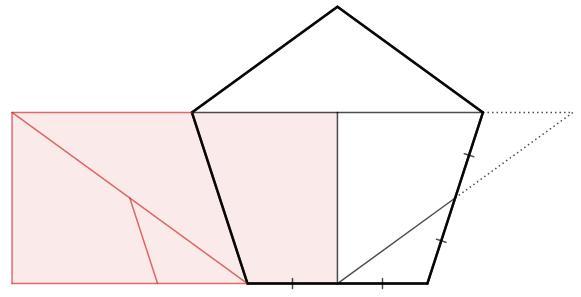
siestarjoki: Правильный пятиугольник: внутренние углы равны, диагонали равны и параллельны соответствующим сторонам.

siestarjoki: Разделим пятиугольник на треугольник и трапецию.
Перенесем треугольник. Сторона треугольника параллельна основанию пятиугольника (т.к. накрест лежащие углы равны), следовательно лежит на продолжении диагонали.

siestarjoki: Разделим трапецию пополам. Превратим половину трапеции в прямоугольный треугольник (стандартное построение). Малый разрез равен половине диагонали, гипотенуза треугольника вдвое больше и равна диагонали - полученный треугольник равен розовому по катету (высота трапеции) и гипотенузе (диагональ пятиугольника).

Вас заинтересует

Химия

1 год назад

які є види агрегатного стану

Алгебра

1 год назад

1.25) 1) √√x² - 2x + 1 = x-1; 2) Va² - ба + 9 = 3-а; 3) Nyt +4y² + 4 = y² +2 тендігі айнымалынын кандай мәндерінде орындалады?

Геометрия

1 год назад

Знайти кути ∆ ABC, якщо кут B у 3 рази менший від кута A і на 45° менший за кут C.

Математика

1 год назад