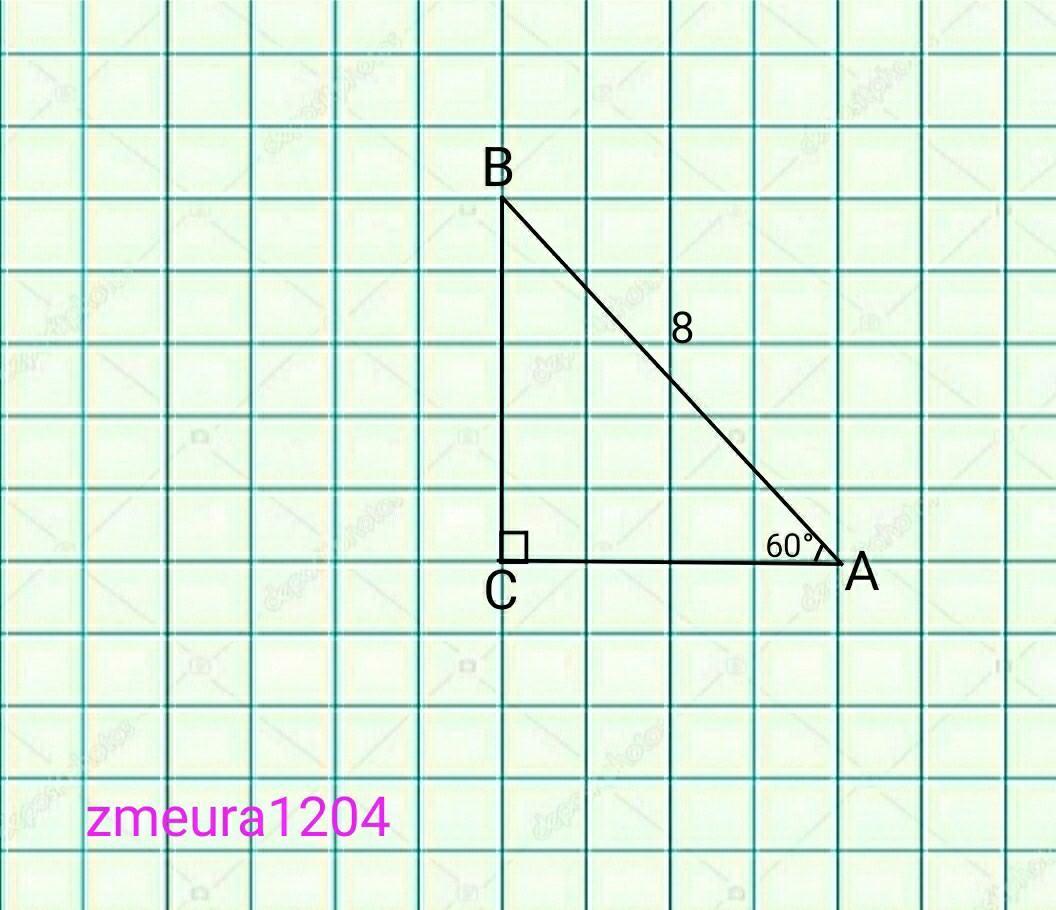
длина гипотенузы АВ прямоугольного треугольника АВС равна 8 см, а величина угла А равна 60°.
Треугольник ABC вращается вокруг самого длинного катета.
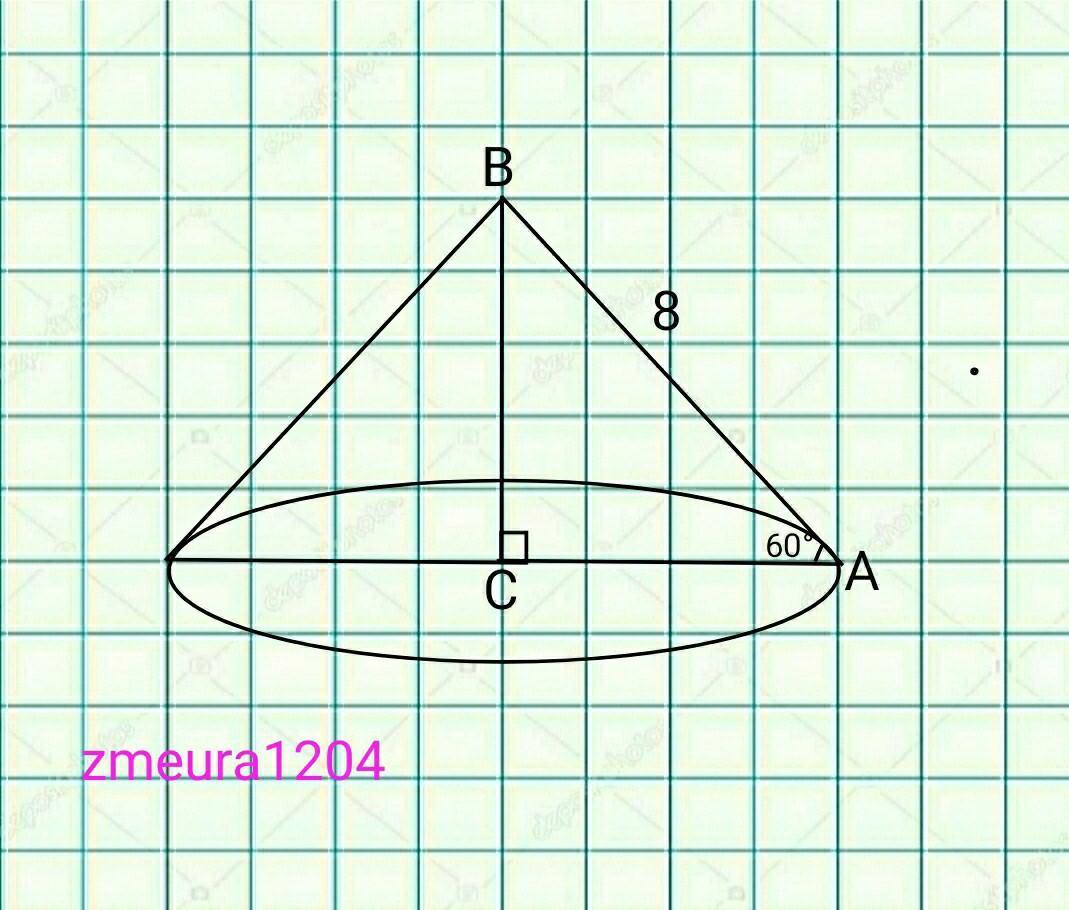
Зарисуйте получившееся тело вращения и рассчитайте его объем.
Ответы
Ответ дал:
1
Ответ:
V=64π√3/3 см³
Объяснение:
∆АВС- прямоугольный треугольник.
∠АВС=90°-∠А=90°-60°=30°.
АС- катет против угла 30°
АС=АВ/2=8/2=4 см
По теореме Пифагора:
ВС=√(АВ²-АС²)=√(8²-4²)=√(64-16)=
=√48=√(3*16)=4√3 см
Большая сторона лежит против большего угла.
Треугольник вращается вокруг ВС.
АС- радиус конуса
ВС- высота конуса
V=⅓*πR²H=⅓*π*4²*4√3=64π√3/3 см³
Приложения:
Вас заинтересует
1 год назад
1 год назад
3 года назад
3 года назад
8 лет назад