Найдите площадь трапеции, основания которой равны 1 и 2, а углы прилежащие к большему основанию равны 30° и 60°
Ответы
Ответ дал:
1
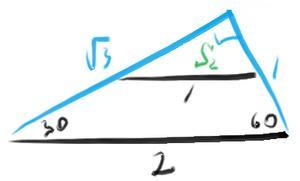
Продлим боковые стороны трапеции до пересечения.
Получим прямоугольный треугольник с углами 30, 60
Катет против угла 30 равен половине гипотенузы =1
Другой катет по т Пифагора =√3
Площадь треугольника S1=√3/2
Основание трапеции 1 параллельно основанию 2 и отсекает подобный треугольник с коэфф подобия 1/2.
Площади подобных фигур относятся как квадрат коэфф подобия.
S2/S1 =1/4
Следовательно площадь трапеции =3/4 S1 =3√3/8
Приложения:
Вас заинтересует
1 год назад
1 год назад
1 год назад
1 год назад
3 года назад
3 года назад