Записать уравнение прямой, которая пересекает прямые (рисунок):
и лежит в плоскости у+z+1=0
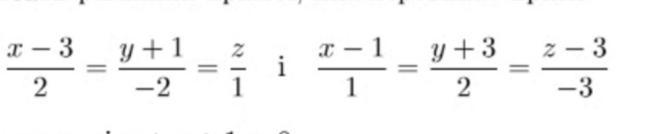
Ответы
Записать уравнение прямой, которая пересекает прямые (рисунок):
и лежит в плоскости у+z+1=0
Находим точки пересечения заданных прямых с заданной плоскостью.
Для этого уравнения прямых представим в параметрическом виде.
Первая прямая:
x = 2t + 3,
y = -2t – 1,
z = t.
Вторая прямая:
x = m + 1,
y = 2m – 3,
z = -3m + 3.
Подставляем в уравнение плоскости у+z+1=0 данные первой прямой.
-2t - 1 + t + 1 = 0,
-t = 0,
t = 0.
Координаты пересечения первой прямой:
x = 2*0 + 3 = 3,
y = -2*0 – 1 = – 1,
z = 0.
А(3; -1; 0).
Подставляем в уравнение плоскости у+z+1=0 данные второй прямой.
2m - 3 – 3m + 3 + 1 = 0,
-m = -1,
m = 1.
Координаты пересечения второй прямой:
x = 1 + 1 = 2,
y = -2*1 – 1 = – 3,
z = 1.
В(2; -3; 1).
Через эти точки и проходит искомая прямая.
Если известны две точки пространства , то уравнения прямой, проходящей через данные точки, выражаются формулами:
Находим вектор АВ = В(2; -3; 1) - А(3; -1; 0) =
= (2 – 3; -3 - (-1); 1 – 0) = (-1; -2; 1).
Получаем искомое уравнение:
(x – 2)/(-1) = (y + 3)/(-2) = (z - 1))/1.