Question

8. Знайти різницю площ вписаного та описаного кіл правильного трикутника, якщо сума радіусів цих кіл дорівнює 12см.​СРООЧНО

Answer 1

Решение.

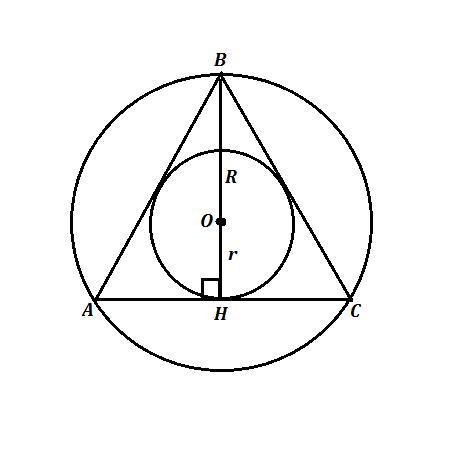
ΔАВC - правильный , АВ=ВС=АС=а , АН ⊥ АС ,  h=AH ,  AH=HB=a/2 ,

R=AO  ,  r=OH  ,  R + r = 12 cм  .

В правильном треугольнике медианы и высоты совпадают, а медианы в точке пересечения делятся в отношении 2 : 1 . Значит и высоты в правильном треугольнике делятся 2 : 1 . Поэтому R : r = 2 : 1

Высоты равны   $h=\sqrt{a^2-\Big(\dfrac{a}{2}\Big)^2}=\dfrac{a\sqrt{3}}{2}$  .

Радиус описанной окружности равен  $R=\dfrac{2}{3}\cdot h=\dfrac{a\sqrt3}{3}$  .

Радиус вписанной окружности равен  $r=\dfrac{1}{3}\cdot h=\dfrac{a\sqrt3}{6}$  .

По условию  R + r = 12 см    ⇒  

$R+r=\dfrac{a\sqrt3}{3}+\dfrac{a\sqrt3}{6}=\dfrac{3a\sqrt3}{6}=\dfrac{a\sqrt3}{2}\ \ ,\ \ \ \dfrac{a\sqrt3}{2}=12\ \ ,\ \ a\sqrt3=24\ \ ,\\\\a=\dfrac{24}{\sqrt3}=\dfrac{24\sqrt3}{\sqrt3\cdot \sqrt3}=8\sqrt3$

Найдём радиусы и посчитаем площади вписанной и описанной окружностей .

$R=\dfrac{a\sqrt3}{3}=\dfrac{8\sqrt3\cdot \sqrt3}{3}=8\ \ ,\ \ \ r=\dfrac{8\sqrt3\cdot \sqrt3}{6}=4\\\\S_1=S_{opisan.}=\pi R^2=64\pi \\\\S_2=S_{vpisan.}=\pi R^2=16\pi \\\\S_1-S_2=64\pi -16\pi =48\pi$  

Ответ:  разность площадей равна  $\boldsymbol{48\pi }$  см² .  

2 способ .  Так как известно, что отношение  АО:ОН=2:1  , то  АО=2х , ОН=х , АН=2х+х=3х .

12=3х  ,  х=4 см ,  2х=8 см  ⇒  R=8 cм  ,  r=4 см

Разность площадей равна   8²π - 4²π = 64π - 16π = 48π  см² .