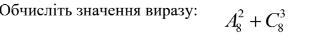Ответы
Ответ дал:
2
Ответ:
Значение выражение:
Примечание:
Число размещений:
Число сочетаний:
Факториал:
Объяснение:
nartajabdullah:
пон
Вас заинтересует
1 год назад
1 год назад
1 год назад
1 год назад
3 года назад
3 года назад
8 лет назад
8 лет назад