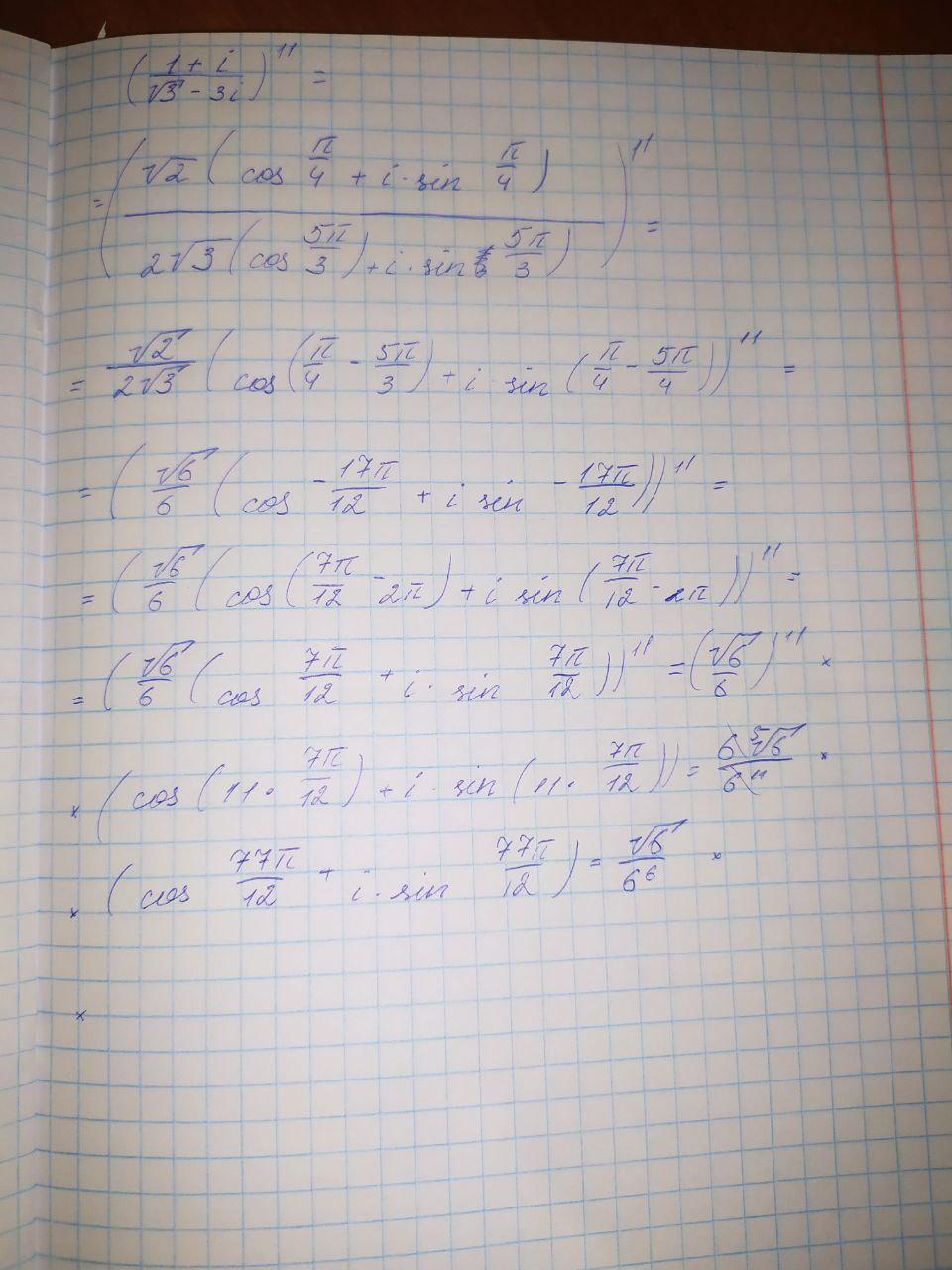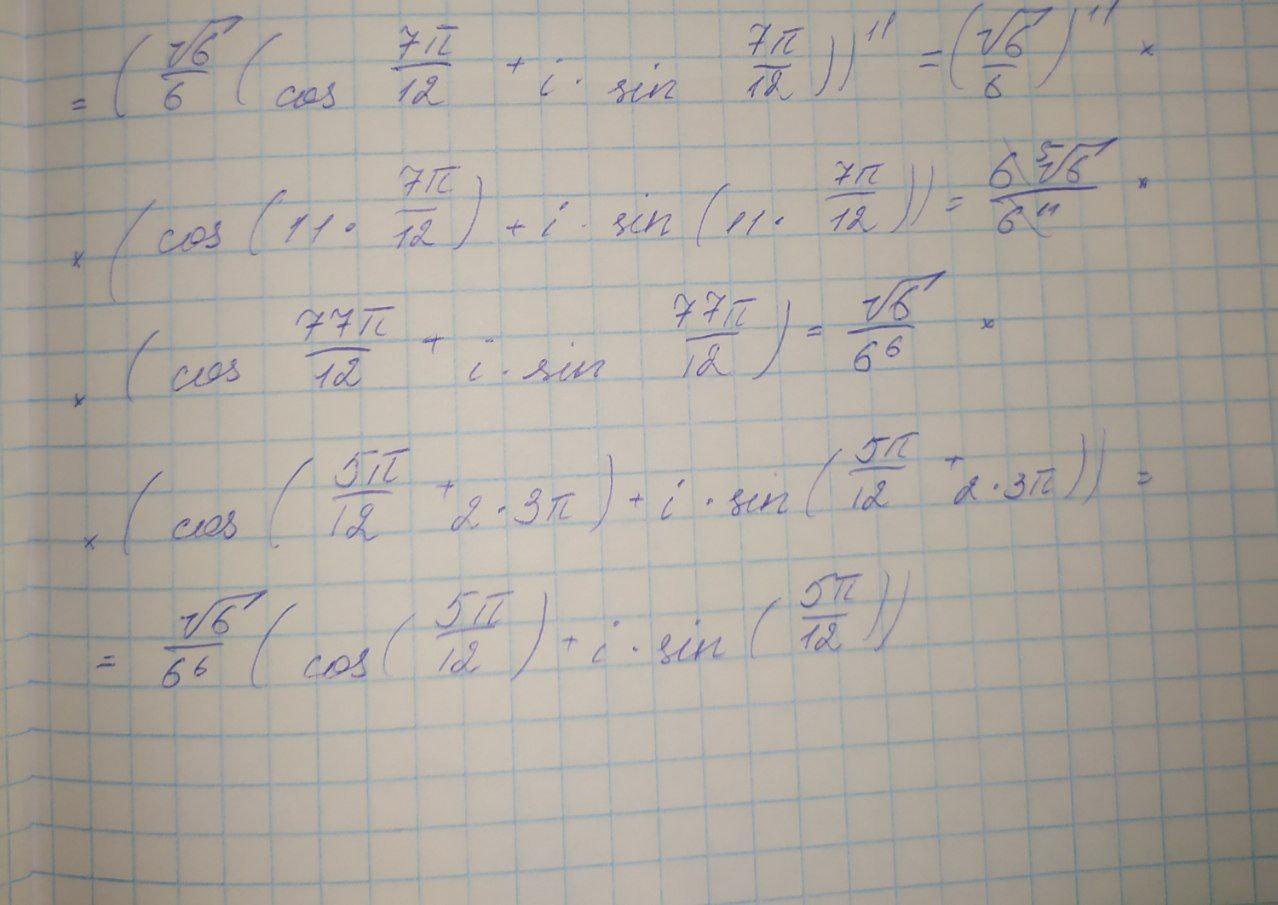Ответы
Ответ дал:
1
Уравнение n-ой степени в комплексных числах имеет n корней.
Извлечение корня из комплексного числа:
В частности, для кубического корня:
Рассмотрим уравнение:
Запишем число в тригонометрической форме.
Найдем его модуль:
Найдем его аргумент, учитывая, что действительная и мнимая части комплексного числа положительны:
Тогда:
Таким образом, уравнение принимает вид:
Извлечем кубический корень:
Ответ:
Вас заинтересует
1 год назад
1 год назад
1 год назад
3 года назад
8 лет назад