Question

23. Прямая на координатной плоскости задана уравнением х - 2y + + 3 = 0. Напишите уравнение прямой, симметричной данной относительно начала координат. ​

Answer 1

Ответ:

$\displaystyle \boxed {x-2y-3=0}$

Объяснение:

23. Прямая на координатной плоскости задана уравнением

х - 2y + 3 = 0.

Напишите уравнение прямой, симметричной данной относительно начала координат. ​

Выразим у:

$\displaystyle 2y=x+3\\\\y=\frac{x}{2}+\frac{3}{2}$

- линейная функция вида y = kx + b, график - прямая.

$\displaystyle \Rightarrow \;\;\; k=\frac{1}{2};\;\;\;b=\frac{3}{2}$

• Для уравнения прямой, симметрично данной, относительно начала координат достаточно поменять знак b на противоположный.

То есть искомая функция будет иметь вид:

$\displaystyle y=\frac{x}{2}-\frac{3}{2}$

или

$\displaystyle 2y=x-3\\\\\boxed {x-2y-3=0}$

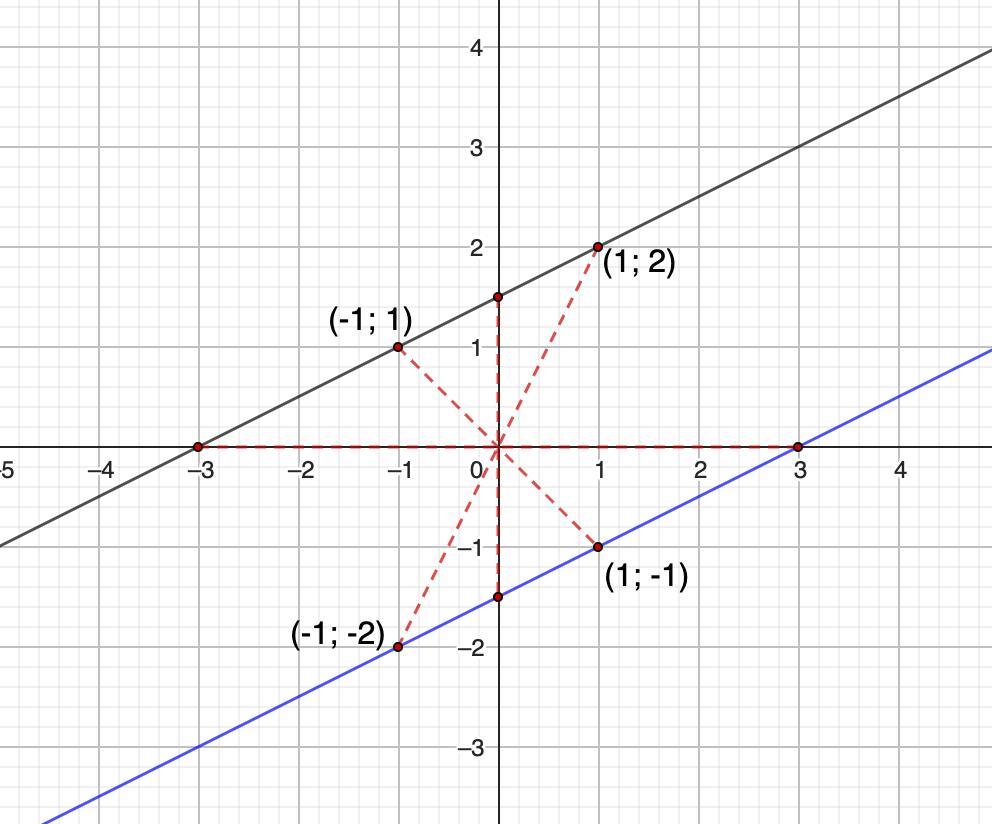
Действительно, если мы возьмем точки на данной прямой, то точки, симметричные началу координат, будут лежать на искомой прямой.

#SPJ1