Question

помогите пожалуйста 50 баллов!​

Answer 1

Ответ:

14. Расстояние от центра окружности до хорды АВ равно 3√3 см.

15. Радиус окружности равен 17 см.

16. Угол D равен 5°.

Объяснение:

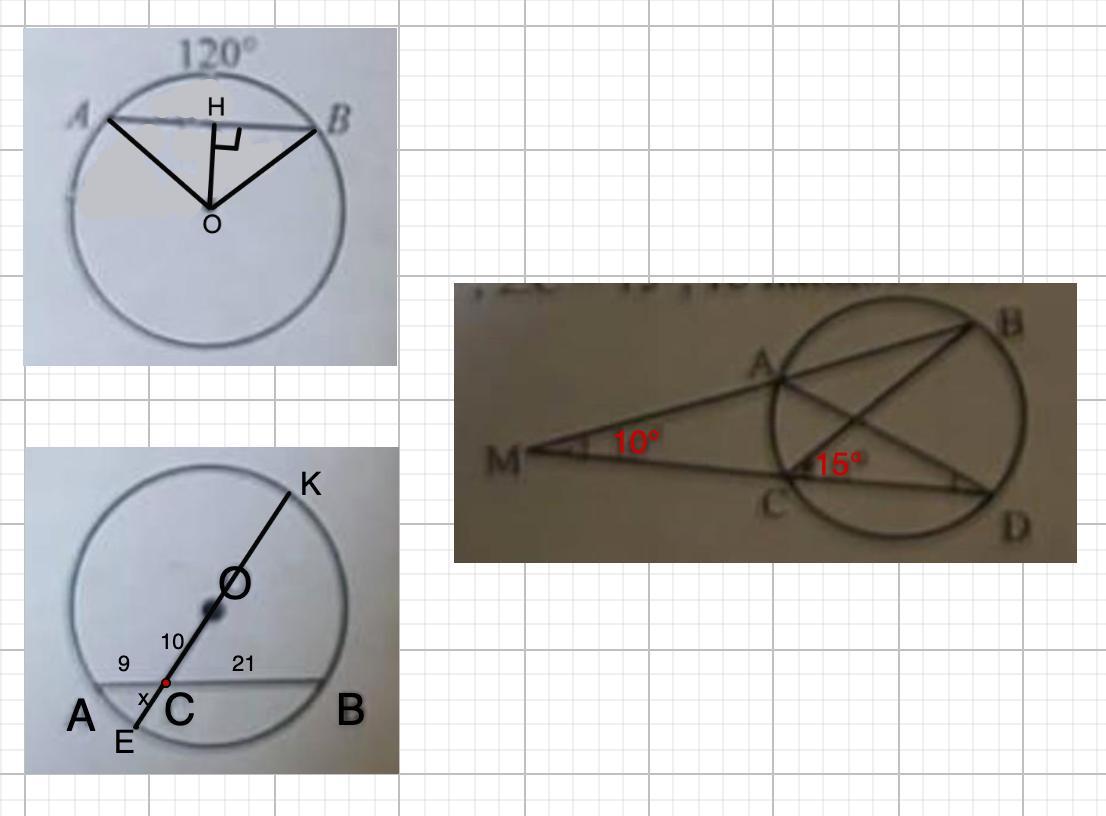
14. Длина хорды АВ = 18 см и ◡AB = 120°. Найдите расстояние от центра окружности до хорды АВ.

15. О - центр окружности. Найдите радиус окружности, если OC = 10 см, АС = 9 см, ВС = 21 см.

16. Если ∠М=10º, ∠С=15°, то найдите ∠D.

15. Дано: Окр.О;

АВ = 18 см - хорда.

Найти: ОН.

Решение:

• Расстояние от точки до прямой - длина перпендикуляра, опущенного из данной точки на данную прямую.

⇒ ОН ⊥ АВ.

• Радиус, перпендикулярный хорде, делит хорду пополам.

⇒ АН = НВ.

Рассмотрим ΔАВО.

ОА = ОВ = R ⇒ ΔАВО - равнобедренный.

• В равнобедренном треугольнике высота, проведенная к основанию, является медианой.

⇒ ОН - высота, медиана.

АН = НВ = 9 см;

• Центральный угол измеряется градусной мерой дуги, на которую он опирается.

⇒ ∠АОВ = ◡АВ = 120°

• В равнобедренном треугольнике углы при основании равны.

⇒ ∠А = ∠В = (180° - 120°) : 2 = 30°

Рассмотрим ΔОАН - прямоугольный.

• Катет, лежащий против угла в 30°, равен половине гипотенузы.

Пусть ОН = х см, тогда ОА = 2х см.

По теореме Пифагора:

ОН² + АН² = ОА²

х² + 81 = 4х²

3х² = 81     |:3

x² = 27

x = 3√3

Расстояние от центра окружности до хорды АВ равно 3√3 см.

15. Дано: Окр.О;

ОС = 10 см; АС = 9 см, ВС = 21 см.

Найти: ОЕ.

Решение:

Пусть СЕ = х см, тогда ОЕ = ОК = (10 + х) см, а СК = (20 + х) см.

• Если две хорды пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой.

⇒ АС · СВ = ЕС · СК

9 · 21 = х · (20 + х)  

$\displaystyle x^2+20x-189=0\\\\D=400+756=1156;\;\;\;\;\;\sqrt{D}=34\\ \\x_1=\frac{-20+34}{2}=7;\;\;\;\;\;x_2=\frac{-20-34}{2}=-27$

x₂ - не подходит по условию задачи.

⇒ ЕС = 7 см

R = ОЕ = 10 + 7 = 17 (см)

Радиус окружности равен 17 см.

16. Дано:   ∠М=10º, ∠С=15°.

Найти: ∠D

Решение:  

• Вписанный угол равен половине градусной меры дуги, на которую он опирается.

⇒ ◡DB = 2∠BCD = 15° · 2 = 30°    

• Угол между двумя секущими проведенными из одной точки измеряется полуразностью заключённых внутри него дуг.

⇒ ∠M = (◡DB - ◡AC) : 2

10° = (30° - ◡AC) : 2

30° - ◡AC = 20°

◡AC = 10°

⇒ ∠D = ◡AC : 2 = 5° (вписанный)

Угол D равен 5°.