Question

Менша сторона прямокутника дорівнює 36. Один iз кутів, утворених діагоналями 120°. Знайти Діаметр описаного кола.Даю 40б

Answer 1

Ответ:

Диаметр описанной окружности равен 72 ед.

Объяснение:

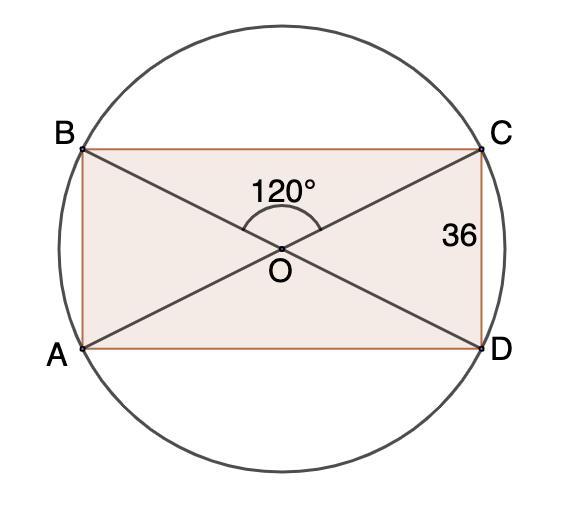
Меньшая сторона прямоугольника равна 36. Один из углов, образованных диагоналями 120°. Найти диаметр описанной окружности.

Дано: ABCD - прямоугольник;

АВ = СD = 36;

∠ВОС = 120°;

Окр.О - описанная около ABCD.

Найти: диаметр Окр.О.

Решение:

∠АВС = 90° - вписанный.

• Прямой вписанный угол опирается на диаметр.

⇒ АС  - диаметр Окр.О.

Рассмотрим ΔАВО.

• Диагонали прямоугольника равны и точкой пересечения делятся пополам.

⇒ АС = BD; AO = OC = BO = OD.

⇒ ΔАВО - равнобедренный.

• Сумма смежных углов равна 180°.

⇒ ∠АОВ = 180° - 120° = 60°

• Если в равнобедренном треугольнике угол, противолежащий основания равен 60°, то этот треугольник равносторонний.

⇒ АВ = ВО = ОА = 36.

Тогда

АС = 2АО = 72 (ед.)

Диаметр описанной окружности равен 72 ед.

#SPJ1