Ответы
Ответ дал:
0
Ответ:
Объяснение:.....
Приложения:
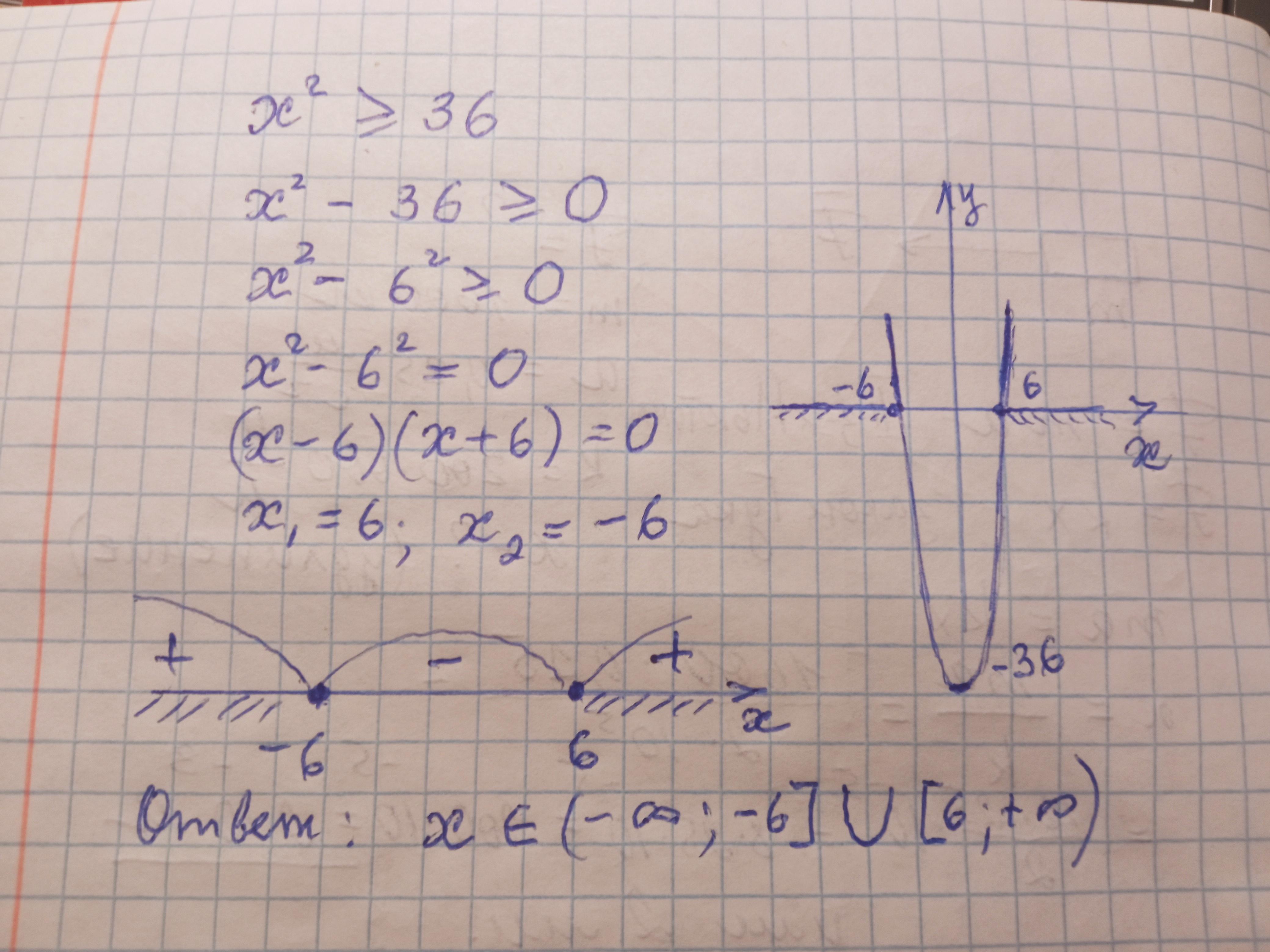
Cohendd:
Метод интервалов.
Ответ дал:
0
Ответ:
(-∞ ; - 6]U[6; + ∞)..
Объяснение:
36 ≤ x²
х² - 36 ≥ 0
(х - 6)(х + 6) ≥ 0
Рассмотрим функцию у = (х - 6)(х + 6)
D(y) = R
Нули функции:
(х - 6)(х + 6) = 0
х = 6 или х = - 6
Отметим на числовой прямой нули функции, определим знаки функции на каждом получившемся промежутке:
_+__[-6]___ - ___[6]__+__ х
у ≥ 0 при х є (-∞ ; - 6]U[6; + ∞).
Ответ: (-∞ ; - 6]U[6; + ∞)..
Приложения:

Вас заинтересует
1 год назад
3 года назад
3 года назад