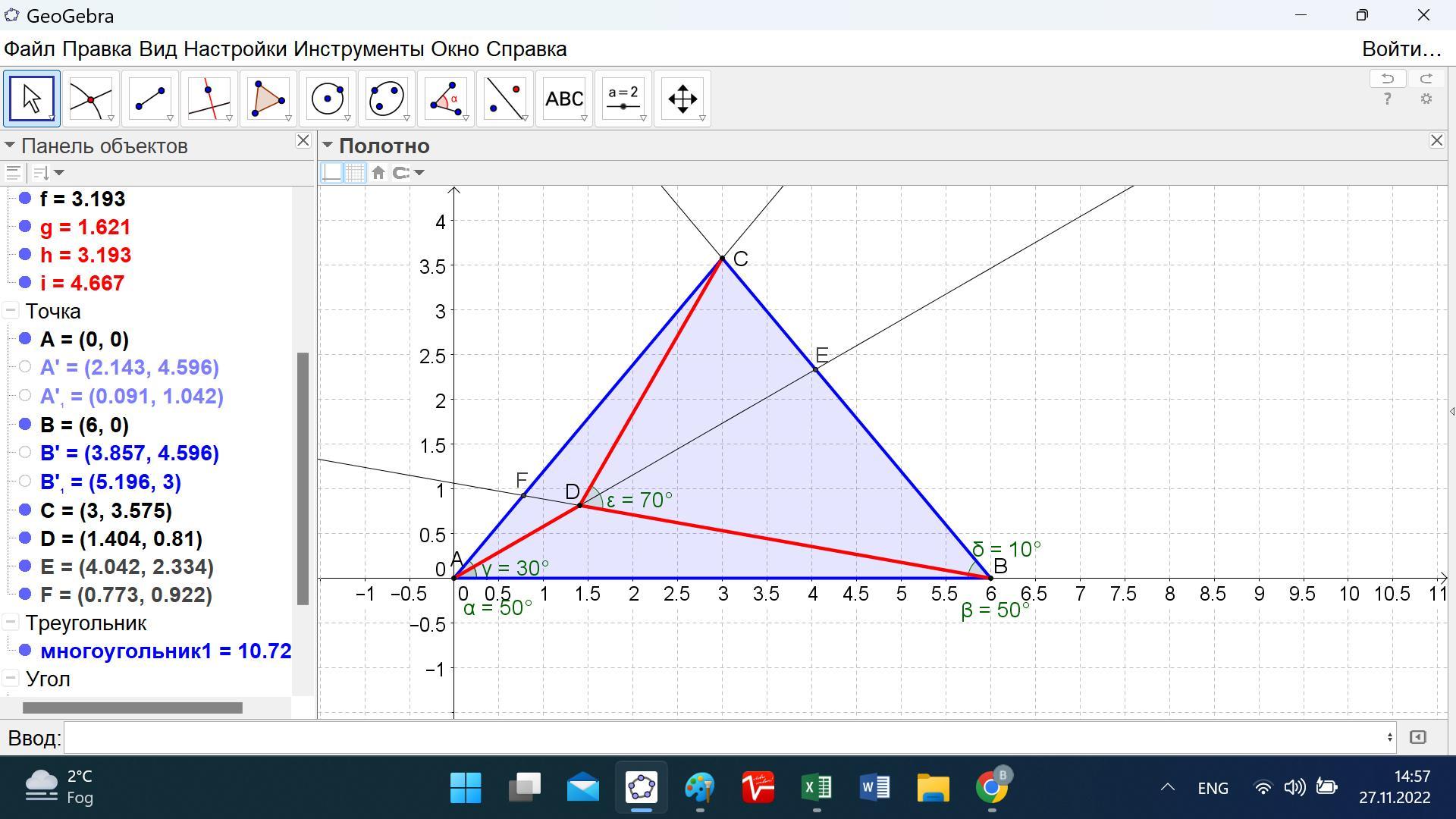
Нужно решить задачу, треугольник равнобедренный, нужной найти угол
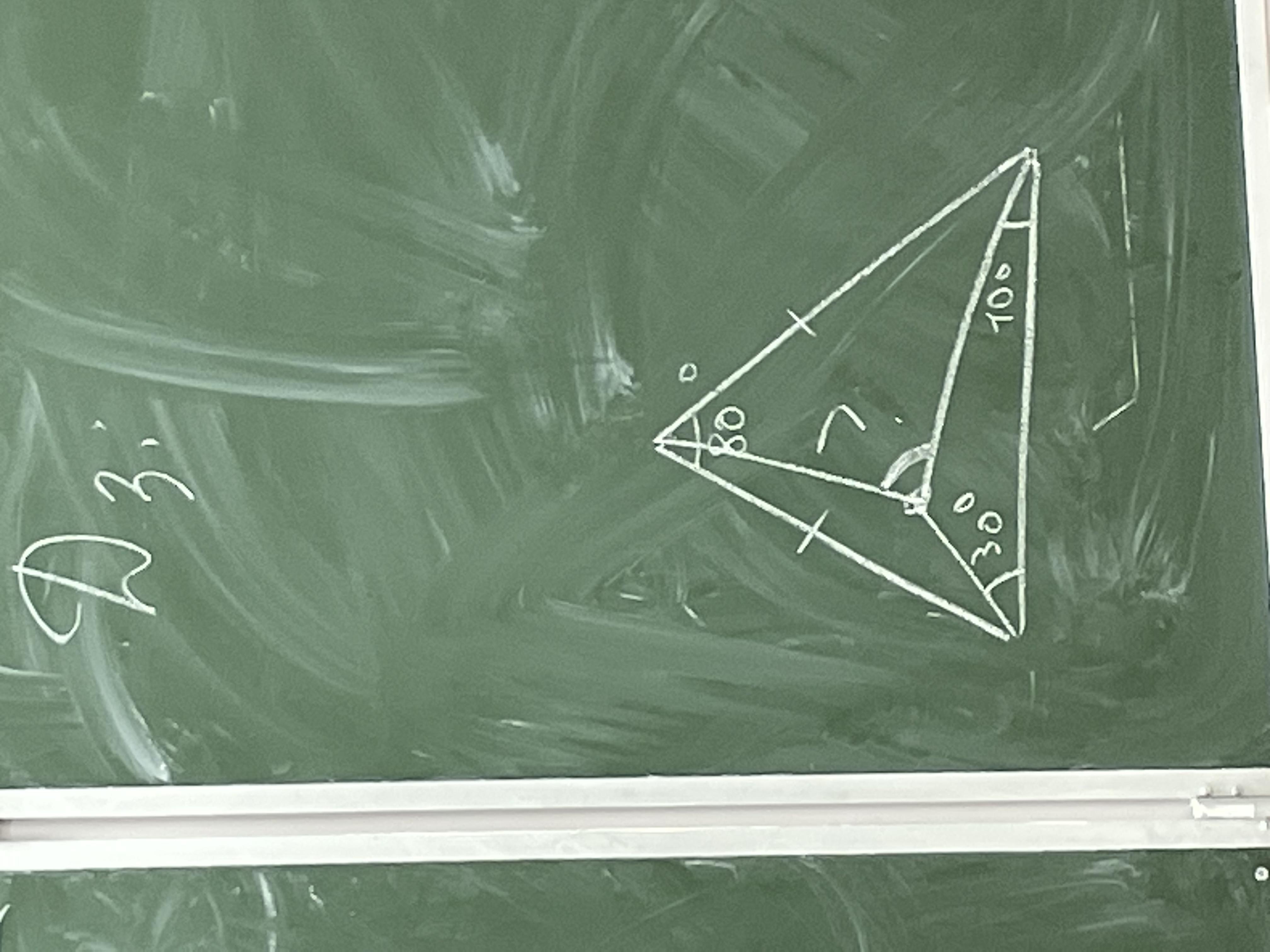
Ответы
Ответ: 70 градусов.
Объяснение:
Примем сторону АВ основания равной 6 ед.
Составим уравнения прямых:
AD = (tg30°)x = (√3/3)x.
BD = (-tg10°)*x + (tg10°)*6 = -0,176326981x + 1,057961884.
Находим координаты точки D как точку пересечения прямых AD и BD, решая равенство:
(√3/3)x = -0,176326981x + 1,057961884.
(0,577350269 + 0,176326981)x = 1,057961884.
x = 1,057961884 / 0,75367725 = 1,403733341
y = 0,810445822
Находим координаты точки С, используя данные рисунка.
х(С) = АВ/2 = 3.
у(С) = (АВ/2)*tg(80°/2) = 3*0,839099631 = 3,575260778.
Находим угловой коэффициент к1 прямой BD.
к1 = Δу/Δх =(0,810445822-0)/( 1,40373334-6) = 0,810445822/-4,596266659 =
-0,176326981.
Находим угловой коэффициент к2 прямой СD.
к2 = Δу/Δх = (0,810445822-3,575260778)/(1,403733341-3) =-2,764814955/(-1,596266659) = 1,732050808.
Тангенс угла α между прямыми ВD и СD равен:
tg α = (k2 – k1)/(1+k1*k2) =(1,732050808-(-0,176326))/(1+(-0,176326)* 1,732050808) = 1,908377788/0,694592711 = 2,747477419.
Угол равен 1,221730476 радиан или 70 градусов.