Question

Бісектриса гострих кутів рівнобічної трапеції перетинаються в точці, яка лежить на меншій основі трапеції. Більша основа трапеції дорівнює 18 см, а бічна сторона 4 см. Знайдіть середню лінію трапеції.
УМОЛЯЮ

Answer 1

Ответ:

Середня лінія трапеції дорівнює 13 см.

Объяснение:

Бісектриса гострих кутів рівнобічної трапеції перетинаються в точці, яка лежить на меншій основі трапеції. Більша основа трапеції дорівнює 18 см, а бічна сторона 4 см. Знайдіть середню лінію трапеції.

• Середньою лінією трапеції називають відрізок, що сполучає середини її бічних сторін.

Властивість середньої лінії трапеції:

• Середня лінія трапеції паралельна до основ і дорівнює їх півсумі.

РОЗВ'ЯЗАННЯ

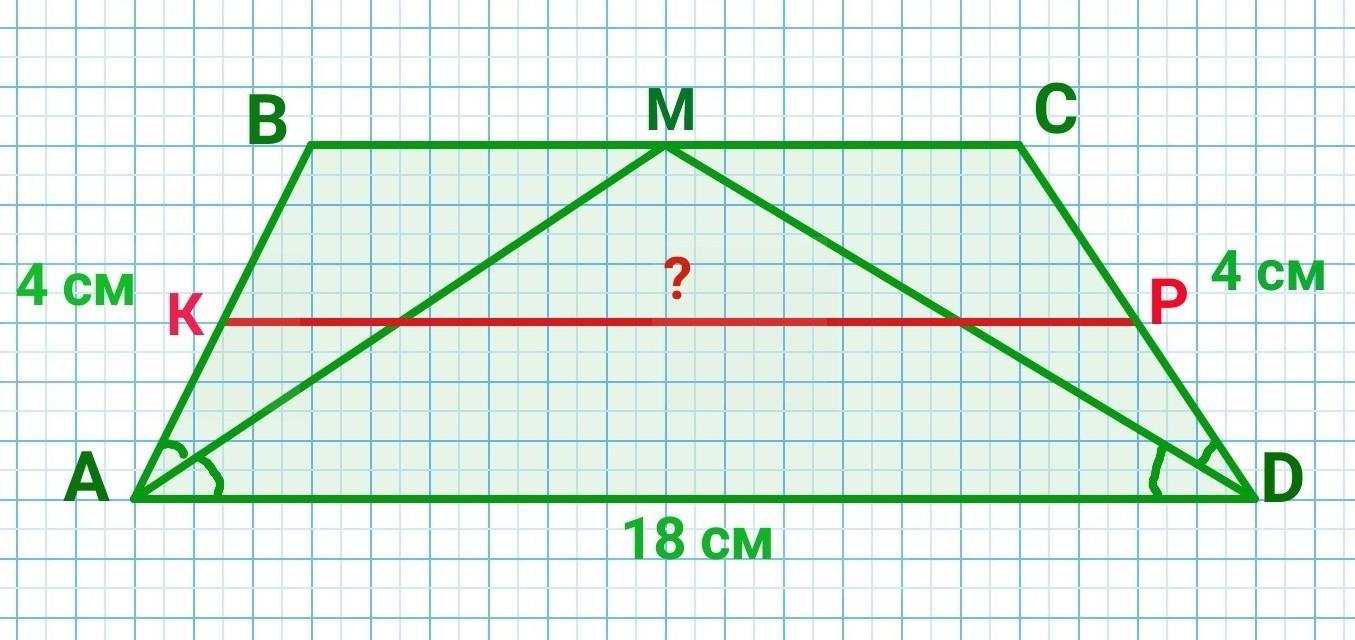
Нехай ABCD - дана трапеція. AD=18 см, AB=CD=4 см, AM - бісектриса кута А ⇒ ∠MAB=∠MAD, DM - бісектриса кута D ⇒∠MDA=∠MDC.

KР - середня лінія.

Знайдемо KР.

1) ∠MAD=∠AМB - як внутрішні різносторонні кути при перетині паралельних прямих BC і AD січною АМ.

∠MAD=∠MAB - за умовою, тому ∠AMB=∠MAB. Отже, △ABM - рівнобедрений з основою АМ (за ознакою рівнобедреного трикутника).

Тому BM=AB= 4 см.

2) ∠MDA=∠DМC - як внутрішні різносторонні кути при перетині паралельних прямих BC і AD січною МD.

∠MDA=∠MDC - за умовою, тому ∠DMC=∠MDC. Отже, △DCM - рівнобедрений з основою МD (за ознакою рівнобедреного трикутника).

Тому MC=CD= 4 см.

3) Довжина меншої основи трапеції дорівнює:

BC=BM+MC=4+4= 8 см

4) Середня лінія трапеції дорівнює:

$KP = \dfrac{BC+AD}{2} = \dfrac{8 + 18}{2} = \bf 13$ см

#SPJ1