Question

Два подібних прямокутних трикутники мають гострий кут 30°. Гіпотенуза одного з них дорівнює меншому катету дру­гого. Визначте коефіцієнт под­ібності трикутників

Answer 1

Розглянемо прямокутний трикутник ABC, у якому:

∠ A — прямий, ∠ B= 30°, отже ∠ C= 60°.

Доведемо, що BC=2AC.


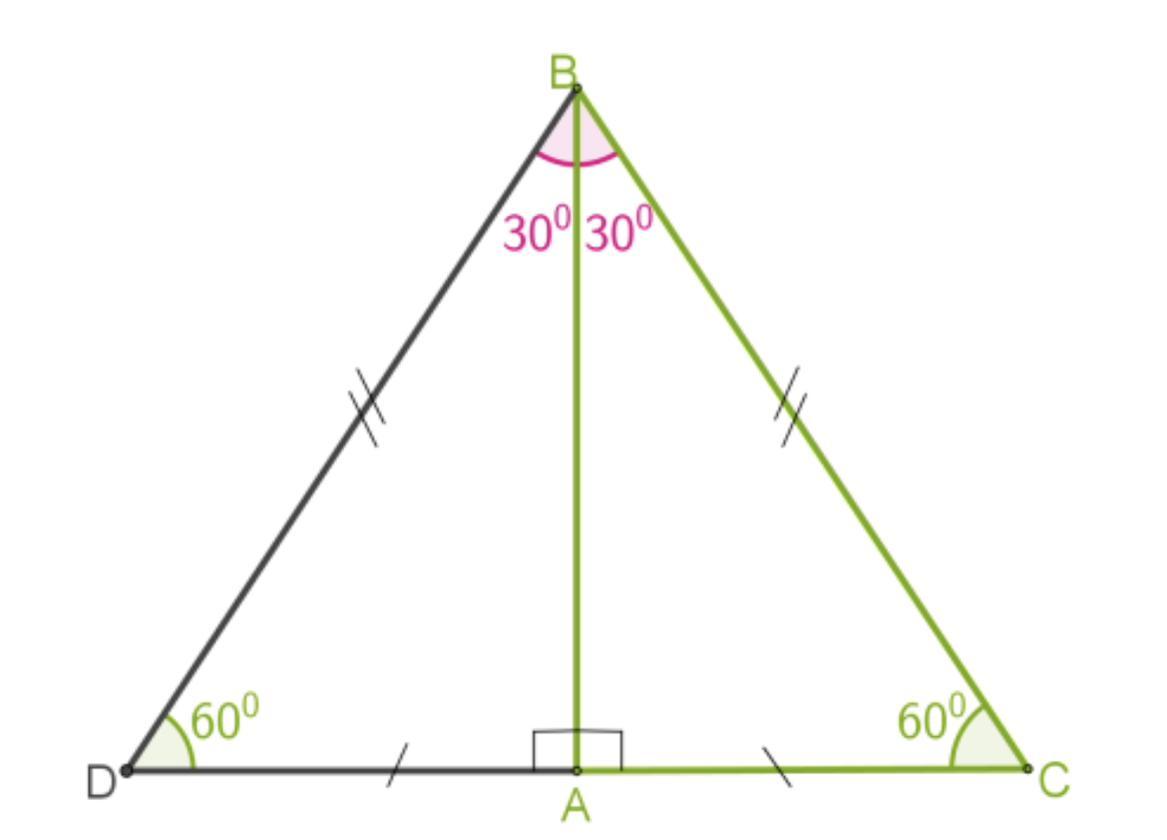
1. Прикладемо до трикутника △ABC рівний йому трикутник △ABD, як показано на рисунку. У них:

∠ C= ∠ D= 60°, як відповідні кути рівних трикутників.

AD=AC, як відповідні сторони рівних трикутників.


2. Отримаємо трикутник △BCD, у якому:

∠ C= ∠ D= 60°, то ∠ B= 60°, за теоремою про суму кутів трикутника.


3. Проти рівних кутів лежать рівні сторони. Звідси BC=DC=BD. Але DC=2AC. Отже, BC=DC=2AC.