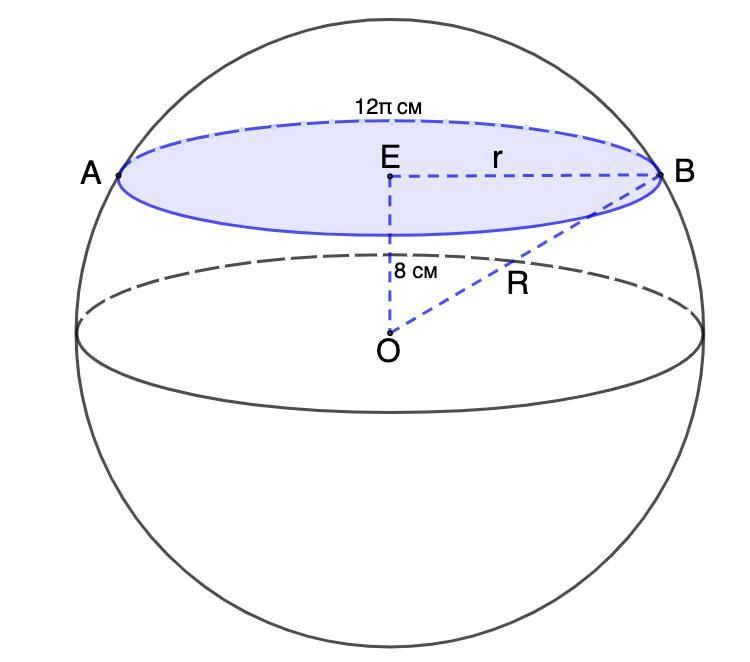
Довжина лінії перетину сфери площиною = 12π. Сферу перетнуто на відстані 8 см від центра. Знайти площу сфери.
Ответы
Ответ дал:
1
Ответ:
Площадь сферы равна 400π см²
Объяснение:
Длина линии пересечения сферы плоскостью = 12π см. Сфера пересечена плоскостью на расстоянии 8 см от центра. Найти площадь сферы.
Дано: сфера (О,R);
Длина линии пересечения сферы плоскостью = 12π см;
Расстояние от центра до плоскости 8 см.
Найти: S сферы
Решение:
- Всякое сечение шара плоскостью есть круг.
⇒ линия пересечения сферы плоскостью есть Окр.(Е,r)
Длина окружности равна:
С = 2πr
C = 12π см (условие)
Подставим в формулу значение С и найдем r:
12π = 2πr ⇒ r = 6 (см)
- Расстояние от точки до плоскости - длина перпендикуляра, проведённого из этой точки к плоскости.
- Если прямая перпендикулярна плоскости, то она перпендикулярна любой прямой, принадлежашей этой плоскости.
⇒ ОЕ ⊥ ЕВ.
Рассмотрим ΔОЕВ - прямоугольный.
ОЕ = 8 см; ЕВ = r = 6 см.
По теореме Пифагора найдем ОВ:
ОВ² = ОЕ² + ЕВ² = 64 + 36 = 100 ⇒ ОВ = √100 = 10 (см)
ОВ = R = 10 см.
Площадь сферы равна:
S сферы = 4πR² = 4π · 100 = 400π (см²)
#SPJ1
Приложения:
Вас заинтересует
1 год назад
1 год назад
1 год назад
3 года назад
3 года назад
8 лет назад
8 лет назад