Question

Терміново!!!
Гіпотенуза прямокутного трикутника дорівнює с, а один із го-стрих кутів дорівнює а. Знайдіть площу бічної поверхні конуса, утвореного в результаті обертання цього трикутника навколо
катета, протилежного даному куту.

Answer 1

Ответ:

Площадь боковой поверхности конуса: S = π·c²·cosa

Объяснение:

Перевод: Гипотенуза прямоугольного треугольника равна с, а один из острых углов равен а. Найдите площадь боковой поверхности конуса, образованного в результате вращения этого треугольника вокруг катета, противоположного данному углу.

Нужно знать: Площадь боковой поверхности конуса вычисляется по формуле: S(б.п.к) = π·R·L, где R — радиус основания конуса, а L — образующая конуса.

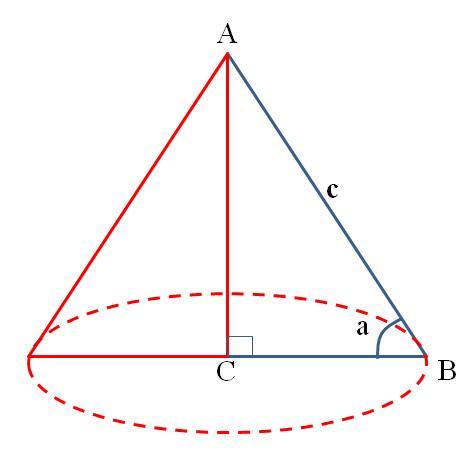
Решение. Рассмотрим прямоугольный треугольник ABC, в котором ∠C = 90°, AB = c - гипотенуза, ∠B = a (см. рисунок).

По условию, треугольник вращается вокруг катета AC и поэтому

BC = R, L = c.

По определению косинуса находим катет BC:

$\displaystyle \tt cosa=\frac{BC}{AB}$ или R = BC = AB·cosa = c·cosa.

Тогда

S(б.п.к) = π·c·cosa·c = π·c²·cosa.

#SPJ1