Question

8. Знайти основи трапеції, середня лiнiя якої дорівнює 34 см. Діагональ трапеції ділить її середню лінію на вiдрiзки, довжини яких відносяться як 6:11.​

Answer 1

Ответ:

Основания трапеции равны 24 см и 44 см.

Объяснение:

8. Найти основы трапеции, средняя линия которой равна 34 см. Диагональ трапеции делит ее среднюю линию на отрезки, длины которых относятся как 6:11.​

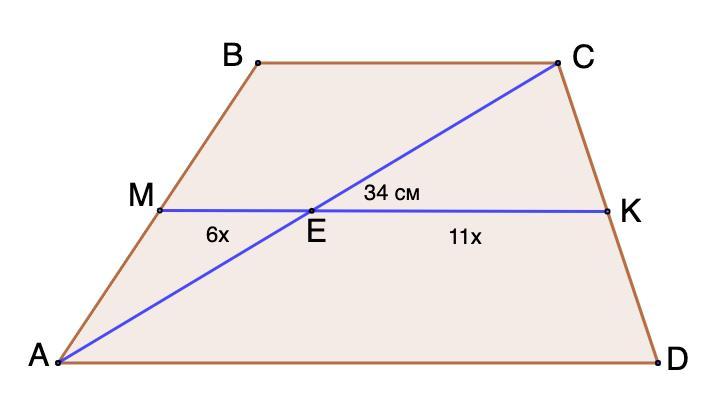
Дано: ABCD - трапеция.

МК = 34 см - средняя линия;

АС ∩ МК = Е;

МЕ : ЕК = 6 : 11.

Найти: ВС и AD.

Решение:

• Средняя линия трапеции равна полусумме оснований и параллельна основаниям.

⇒ ВС + AD = 34 · 2 = 68 (см)

МЕ : ЕК = 6 : 11

Пусть МЕ = 6х см; ЕК = 11х см.

1. Рассмотрим ΔАВС.

АМ = МВ (МК - средняя линия.)

МЕ || ВС (МК - средняя линия.)

• Признак средней линии треугольника: если отрезок в треугольнике проходит через середину одной из его сторон, пересекает вторую и параллелен третьей — этот отрезок можно назвать средней линией этого треугольника.

⇒ МЕ - средняя линия ΔАВС.

МЕ = 6х см, ⇒ ВС = 12х см.

2. Рассмотрим ΔАСD.

CK = KD (МК - средняя линия.)

EK || AD (МК - средняя линия.)

⇒ ЕK - средняя линия ΔАСD.

ЕK = 11х см, ⇒ ВС = 22х см.

3. ВС + AD = 68 (см)

12x + 22x = 68

34x = 68   |:34

x = 2

⇒ BC = 2 · 12 = 24 (см)

AD = 2 · 22 = 44 (см)

Основания трапеции равны 24 см и 44 см.

#SPJ1