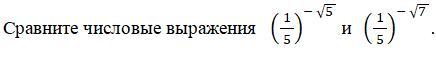Question

Помогите с заданием по алгебре (с объяснением)

Answer 1

Ответ:

$\left( \dfrac{1}{5} \right) {}^{ - \sqrt{5}} <\left( \dfrac{1}{5} \right) {}^{ - \sqrt{7}}$

Объяснение:

Сравните числовые выражения $\boldsymbol{\left (\dfrac{1}{5} \right )^{-\sqrt{5}}}$ и $\boldsymbol{\left (\dfrac{1}{5} \right )^{-\sqrt{7}}}$

Запишем данные выражения в удобном виде - используя свойство степеней : $a^{-n}= \frac{1}{a^n}$.

$\displaystyle \left( \dfrac{1}{5} \right) {}^{ - \sqrt{5} } = \frac {1}{ \frac{1}{5 {}^{ \sqrt{5} } }} = 5 {}^{ \sqrt{5} }$

$\displaystyle \left( \dfrac{1}{5} \right) {}^{ - \sqrt{7} } = \frac{1}{ \frac{1}{5 {}^{ \sqrt{7} } } } = 5 {}^{ \sqrt{7} }$

Сравним $\underline{5^{\sqrt{5}}}$ и $\underline{5^{\sqrt{7}}}$.

Обратим внимание , выражения с одинаковым основанием , значит , нужно сравнить только показатели степеней , $\sqrt{5}<\sqrt{7}$ т.к $5<7$ , тогда $5^{\sqrt{5}}<5^{\sqrt{7}} \Rightarrow$

$\boxed{ \boldsymbol{ \left( \dfrac{1}{5} \right) {}^{ - \sqrt{5}} <\left( \dfrac{1}{5} \right) {}^{ - \sqrt{7}} }}$