Бісектриса кута паралелограма ділить його сторону на відрізки
довжиною 10 см і 12 см, починаючи від найдальшої до цього кута вершини.
Знайдіть периметр паралелограма.
Ответы
Ответ дал:
1
Ответ:
Периметр паралелограма дорівнює 68 см
Объяснение:
Бісектриса кута паралелограма ділить його сторону на відрізки довжиною 10 см і 12 см, починаючи від найдальшої до цього кута вершини. Знайдіть периметр паралелограма.
- Периметр паралелограма дорівнює подвоєної сумі двох суміжних сторін:
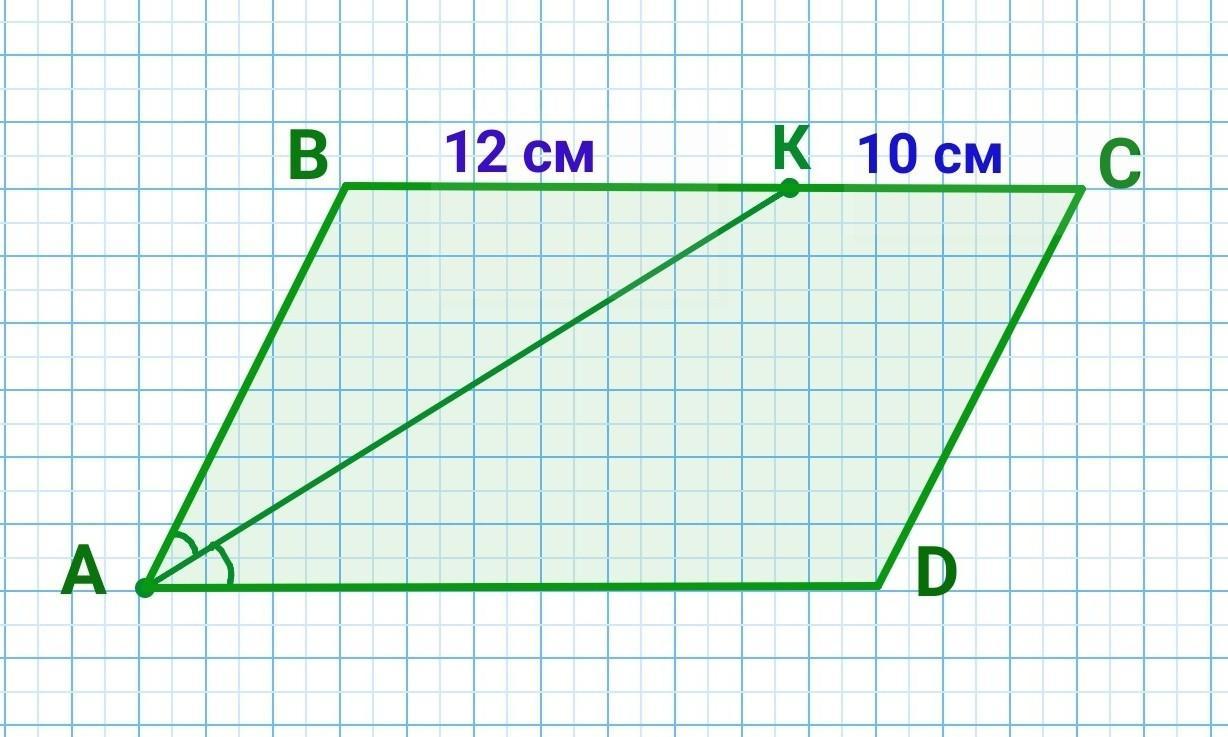
Дано: ABCD - паралелограм, АК - бісектриса кута А, ВК=12 см, KC=10 см
Знайти: Р(ABCD)
Розв'язання
1) BC =BK+KC=12+10= 22 (см)
2) ∠KAD=∠BKA - як внутрішні різносторонні кути при перетині паралельних прямих BC і AD січною AK.
∠KAD=∠BAK - за умовою, тому:
∠BKA=∠BAK.
Отже, за ознакою рівнобедреного трикутника: △ABK - рівнобедрений з основою AK,
AB=BK= 12 (см) - як бічні сторони рівнобедреного трикутника.
3) Р(ABCD)=2•(12+22)=2•34= 68 (см)
#SPJ1
Приложения:
Вас заинтересует
1 год назад
3 года назад
3 года назад
8 лет назад