Question

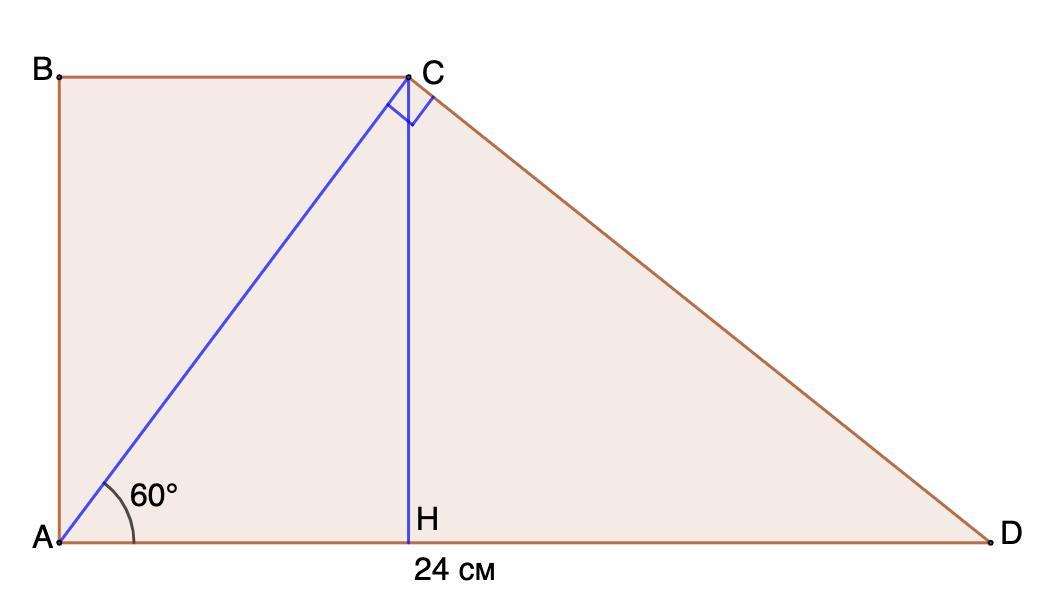
3.Диагональ АС прямоугольной трапеции ABCD перпендикуляр на боковой стороне CD и составляет угол в 60° с основанием AD. Найдите площадь трапеции, если AD = 24 см.
Пожалуйста без синусов и косинусов

Answer 1

Ответ:9√3

Объяснение:

Answer 2

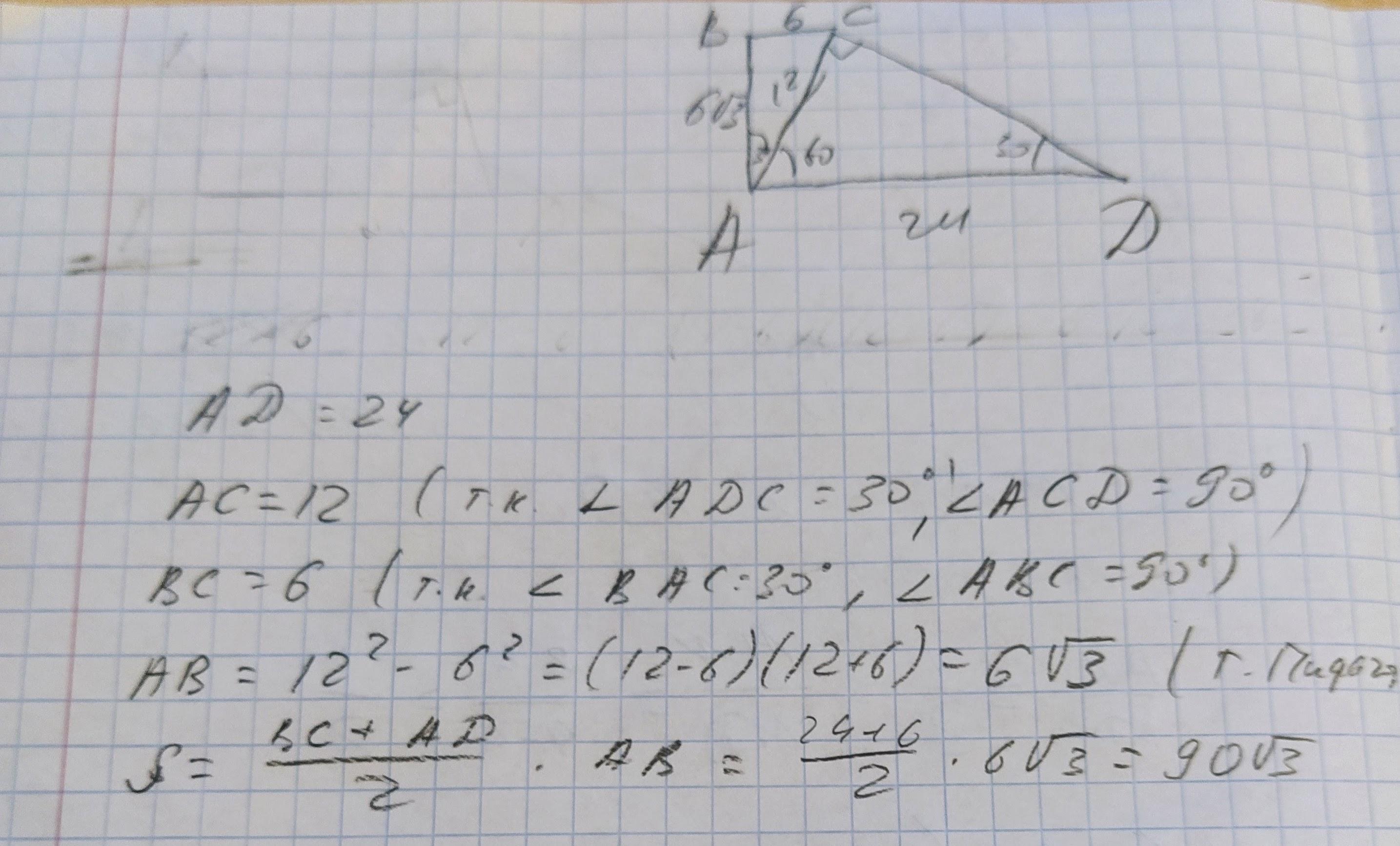
Ответ:

Площадь трапеции равна 90√3 см².

Объяснение:

3. Диагональ АС прямоугольной трапеции ABCD перпендикулярна боковой стороне CD и составляет угол в 60° с основанием AD. Найдите площадь трапеции, если AD = 24 см.

Дано: ABCD - прямоугольная трапеция;

АС - диагональ; АС ⊥ CD;

∠CAD = 60°; AD = 24 см

Найти: S(ABCD)

Решение:

• Площадь трапеции равна произведению полусуммы оснований на высоту.

⇒ Необходимо найти основание ВС и высоту СН.

1. Рассмотрим ΔACD - прямоугольный.

∠CAD = 60°.

• Сумма острых углов прямоугольного треугольника равна 90°.

⇒ ∠D = 90° - 60° = 30°

• Катет, лежащий против угла в 30°, равен половине гипотенузы.

⇒ АС = AD : 2 = 24 : 2 = 12 (см)

2. Рассмотрим ΔАСН - прямоугольный.

∠АСН = 90° - 60° = 30°

⇒ АН = АС : 2 = 12 : 2 = 6 (см) (катет, лежащий против угла в 30°)

Теорема Пифагора : квадрат гипотенузы равен сумме квадратов катетов.

⇒ АС² = АН² + СН²

СН² = АС² - АН² = 144 - 36 = 108  ⇒ СН = √108 = 6√3 (см)

Высота равна 6√3 см.

3. Рассмотрим АВСН.

ВС || АН (ABCD - трапеция.

ВА ⊥ AD (условие); СН ⊥ AD (построение)

• Если две прямые перпендикулярны третьей, то они параллельны между собой.

⇒ ВА || СН

АВСН - прямоугольник.

• Противоположные стороны прямоугольника равны.

⇒ ВС = АН = 6 (см)

Меньшее основание равно 6 см.

Ищем площадь:

$\displaystyle S(ABCD) = \frac{BC+AD}{2} \cdot CH=\frac{6+24}{2}\cdot 6\sqrt{3} =90\sqrt{3}$ (см²)

Площадь трапеции равна 90√3 см².