Question

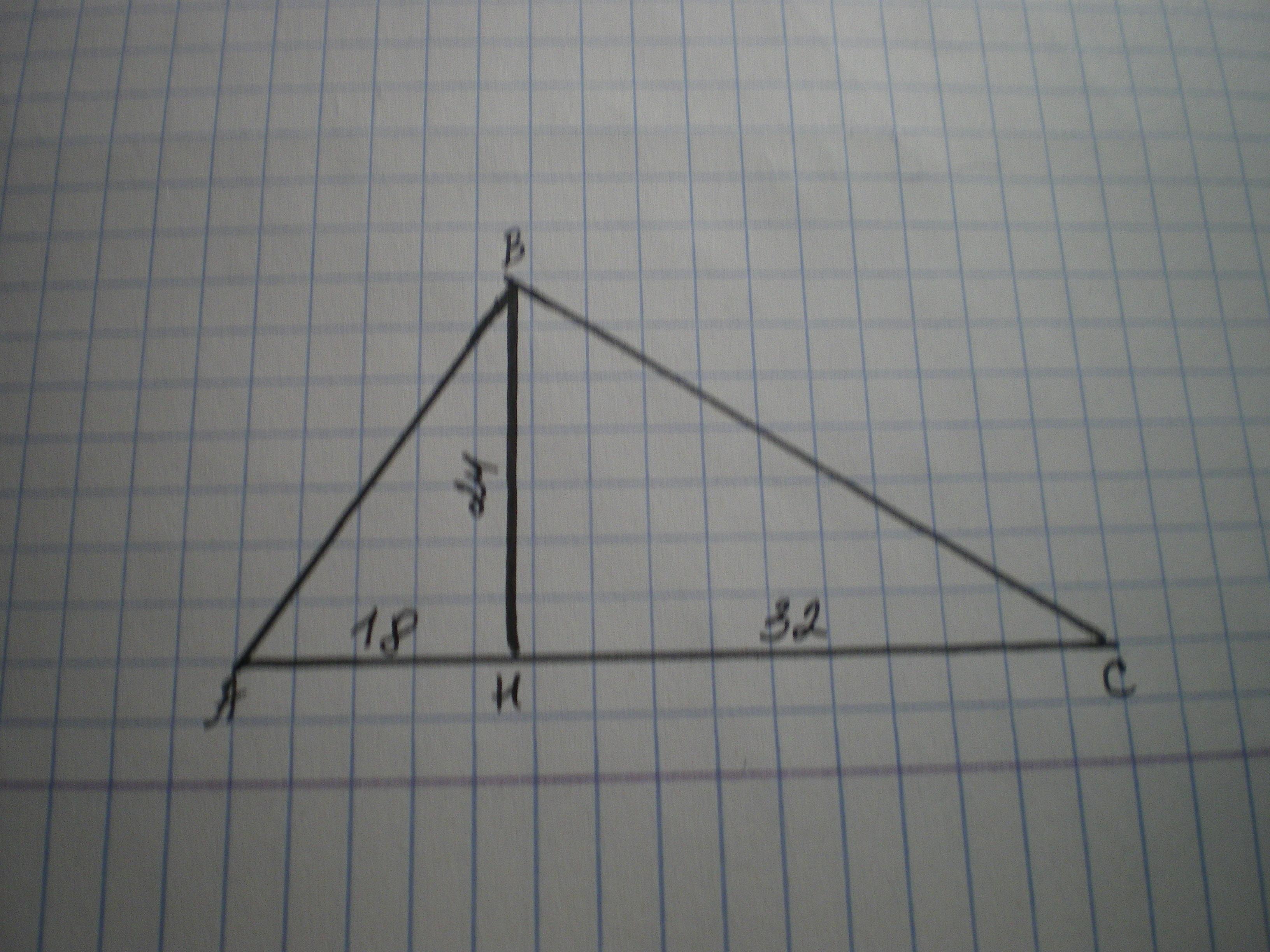
Высота
прямоугольного треугольника, проведенная к гипотенузе, делит ее на отрезки
длиной 18 см и 32 см. Найти катеты треугольника.


(Напишите, пожалуйста, полный ответ)

Answer 1

высота, опущенная из прямого угла является средним геометрическим отрезков гипотенузы на которые она разделилась. гипотенуза равна 18+32=50, h=√18*32=√9*2*16*2=3*2*4=24, по соотношениям в прямоугольном треугольнике катет а=√50*32=√25*2*16*2=5*2*4=40, катет b=√50*18=25*2*9*2=5*3*2=30

Answer 2

Ответ:

30 см, 40 см.

Объяснение:

Дано: ΔАВС - прямоугольный, ∠АВС=90°, ВН - высота, АН=18 см, СН=32 см. Найти АВ и ВС.

Высота в прямоугольном треугольнике, проведенная из вершины прямого угла, разбивает прямоугольный треугольник на два подобных треугольника.

ΔАВН подобен ΔСВН, из чего следует, что

ВН=√(АН*НС)=√(18*32)=√576=24 см.

По теореме Пифагора

АВ=√(АН²+ВН²)=√(324+576)=√900=30 см.

ВС=√(ВН²+СН²)=√(576+1024)=√1600=40 см.